树的存储表示、树和二叉树以及森林的相互转换、树和森林的深度优先遍历和广度优先遍历

一.  树的存储表示

对于多叉树来说，因为其每个结点的分支树可能不相等，所以存储会更复杂一些，常用的存储方式有以下四种

1.  广义表表示法

利用广义表来表示一棵树，在树中的，结点可以分为3种：叶节点、根结点、分支节点（除了根结点、分支节点以外的其他结点）

在广义表中，也可以有三种结点与之相对应：原子结点、表头结点、子表结点

举例：用广义表表示法表示下图：

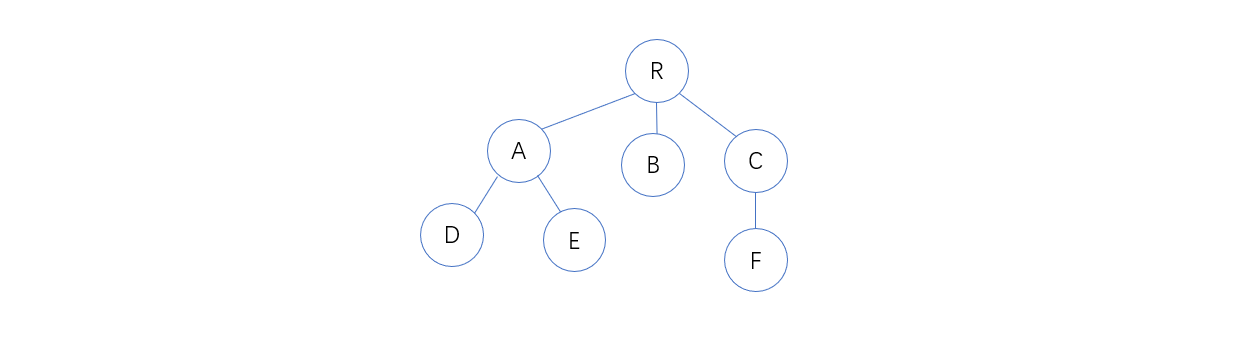
1.1  首先写出根结点：R

1.2  在括号中，写出根结点的子女结点：R（A，B，C）

1.3  在括号中，分别写出A、C结点的子女结点：R（A（D，E），B，C（F））

1.4  在括号中，写出F结点的子女结点：R（A（D，E），B，C（F（G，H，K）））

2.  父指针表示法

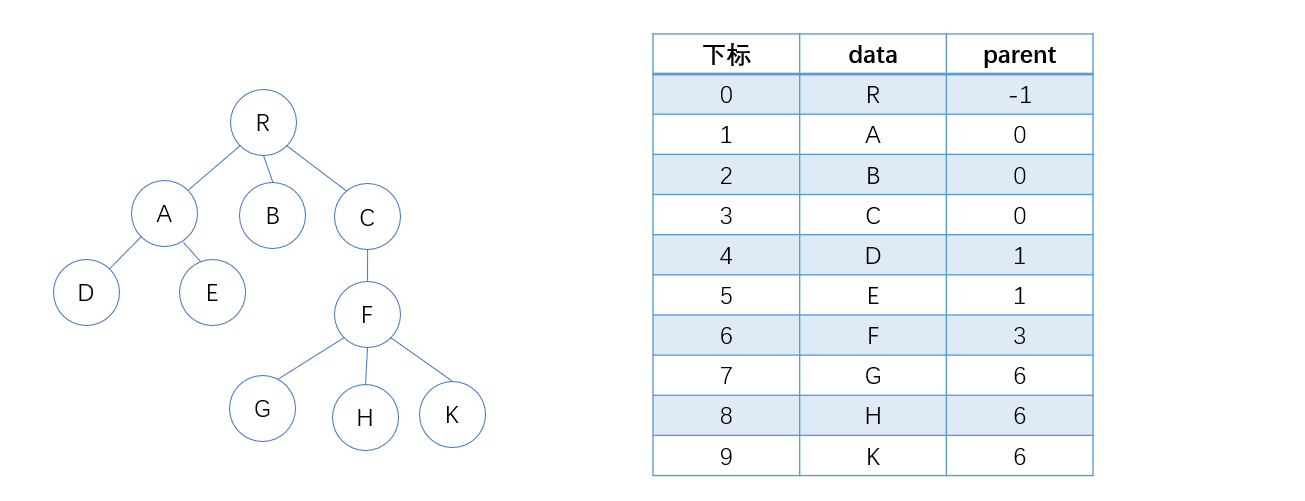
父指针表示法又称双亲表示法：用一组连续的空间来存储树中的结点，在保存每个结点的同时附设一个指示器来指示其双亲结点在表中的位置，如下图：

双亲表示法的优点：利用了树中每个结点（根节点除外），只有一个双亲结点的性质，使得查找双亲结点非常方便

双亲表示法的缺点：在求某个结点的孩子的时候，需要遍历整个向量，所以可以用下面的子女链表表示法

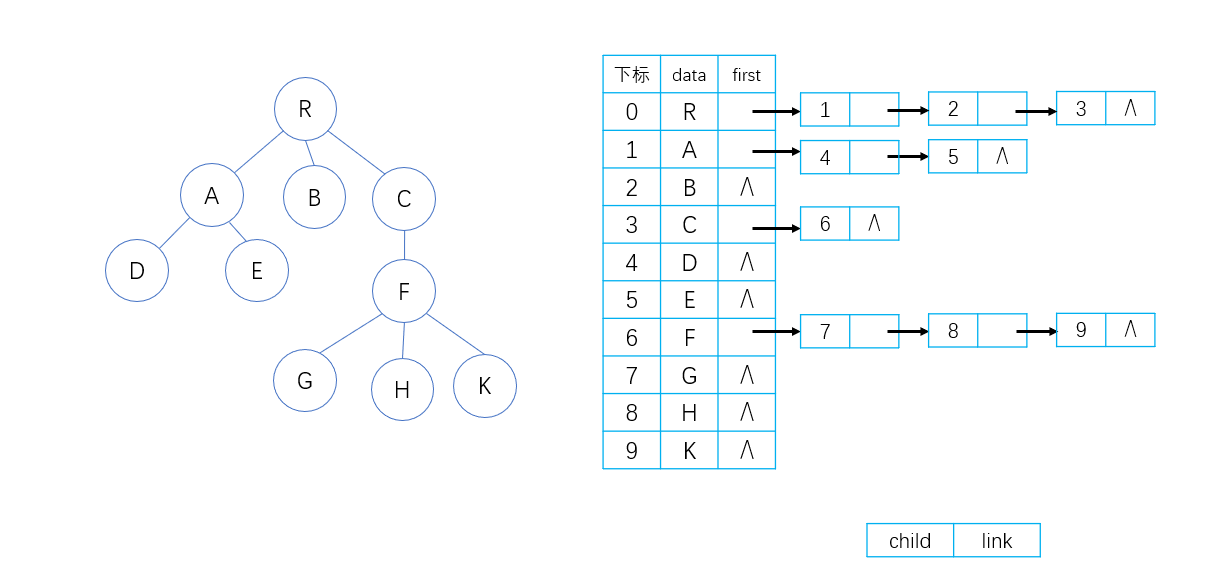
3.  子女链表表示法

子女链表表示法又称孩子表示法：每个结点的孩子结点构成一个单链表，即孩子链表n个结点共有n个孩子链表，

n个结点的数据和n个孩子链表的头指针组成一个顺序表

如下图：

4.  子女-兄弟链表示法

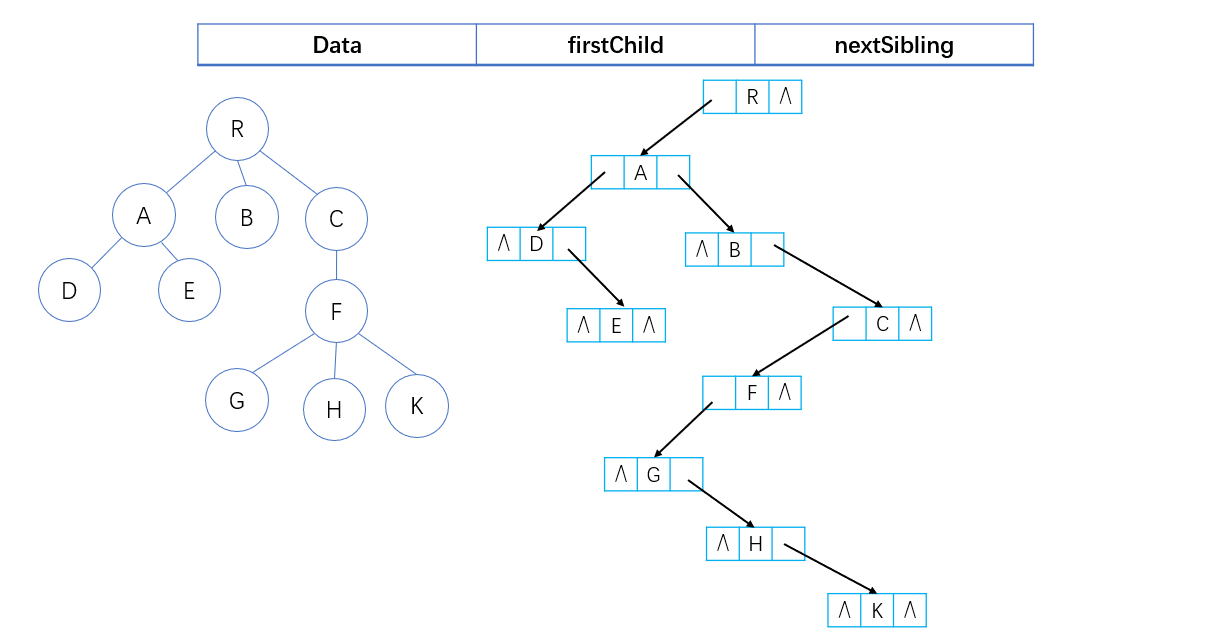
子女-兄弟链表示法又称孩子兄弟表示法、左子右兄表示法：链表中每个结点有两个链域：分别指向该节点的第一个孩子结点和下一个右兄弟结点，它的每个结点的度为2，是最节省存储空间的树的存储表示。如下图：

步骤讲解：

4.1  R是根结点，只有子，没有兄弟，所以将fistChild指向A，nextSibing为空

4.2  A的左子为D，右兄为B，所以将fistChild指向D，nextSibing指向B

4.3  D没有子，右兄为E，所以将fistChild为空，nextSibing指向E

4.4  E没有子，也没有兄，所以将fistChild为空，nextSibing为空

4.5  B没有子，右兄为C，所以将fistChild为空，nextSibing指向C

4.6  C没有兄，但是有子为F，所以将fistChild指向F，nextSibing为空

4.7  F没有兄，但是有左子为G，所以将fistChild指向G，nextSibing为空

4.8  G没有子，右兄为H，所以将fistChild为空，nextSibing指向H

4.9  H没有子，右兄为K，所以将fistChild为空，nextSibing指向K

4.10  K没有子，没有兄，所以将fistChild为空，nextSibing为空

二.  树转换为二叉树

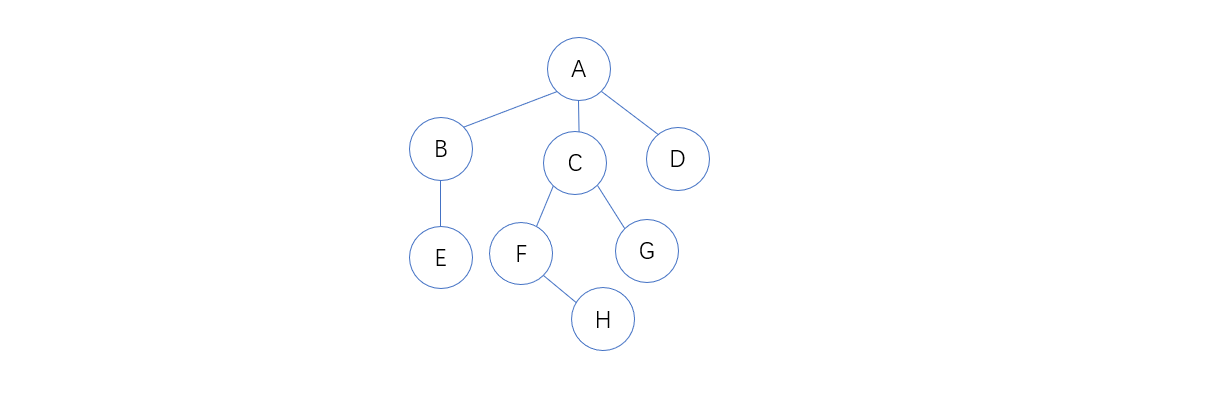
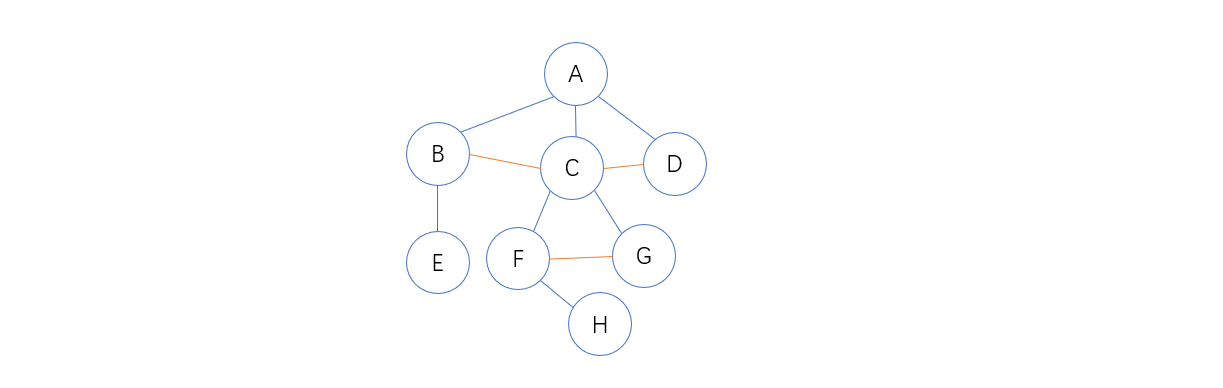
以下图为例：

1.  树中所有相邻的兄弟互相连线（下图中红色为该连线）

2.  对树中的每个节点，只保留其与第一个孩子的结点之间的连线，删去与其他孩子之间的连线

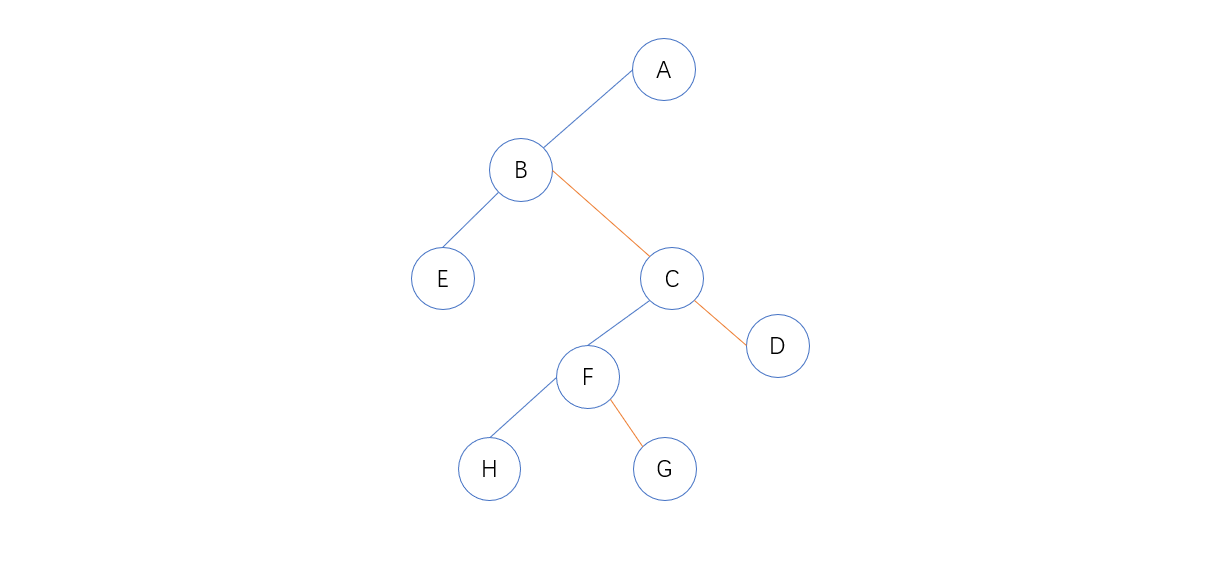
3.  以树的根结点为轴心，将整棵树顺时针旋转一定的角度，使之结构分明（也就是上图的每个父结点的左子右兄在同一层），转换完成

我们可以看出：

树中的某个结点的第一个孩子在二叉树中是相应结点的左孩子

树中的某个结点的右兄弟结点在二叉树中是相应结点的右孩子

也就是，在二叉树中，左分支上的各节点在原来的树中是父子关系，而右分支上的各节点在原来的树中是兄弟关系

三.  森林转换为二叉树

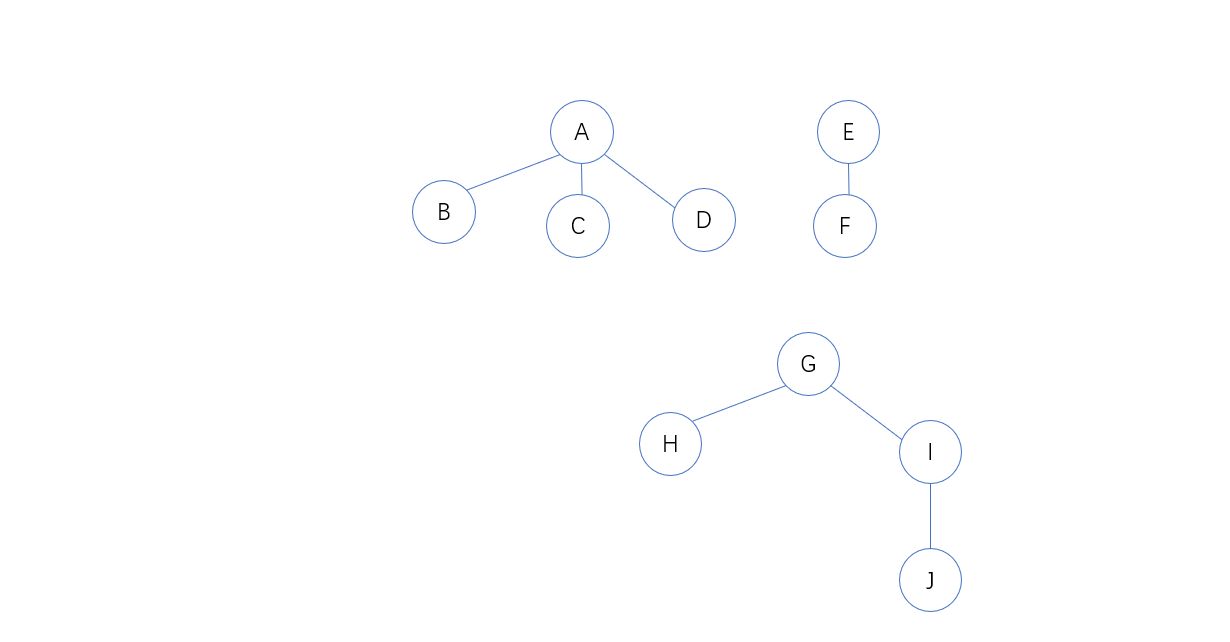
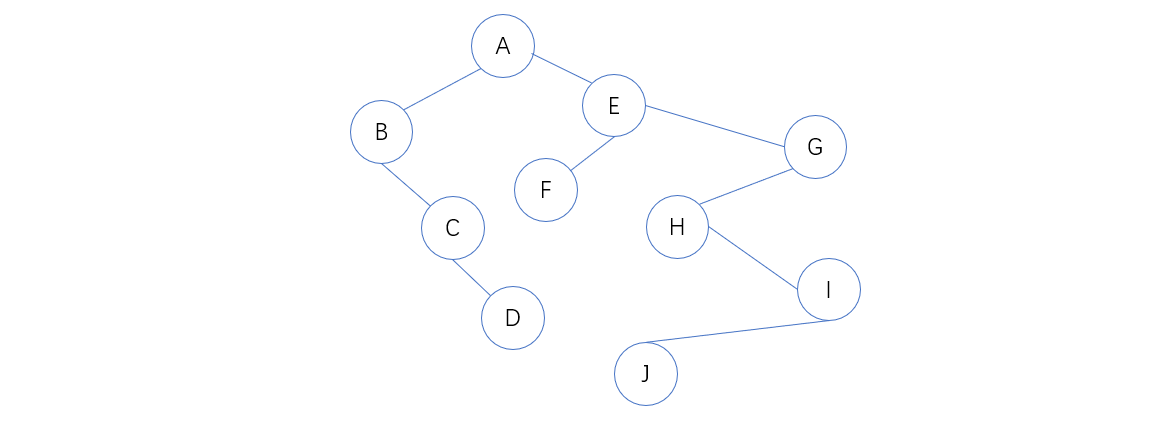
以下图为例：

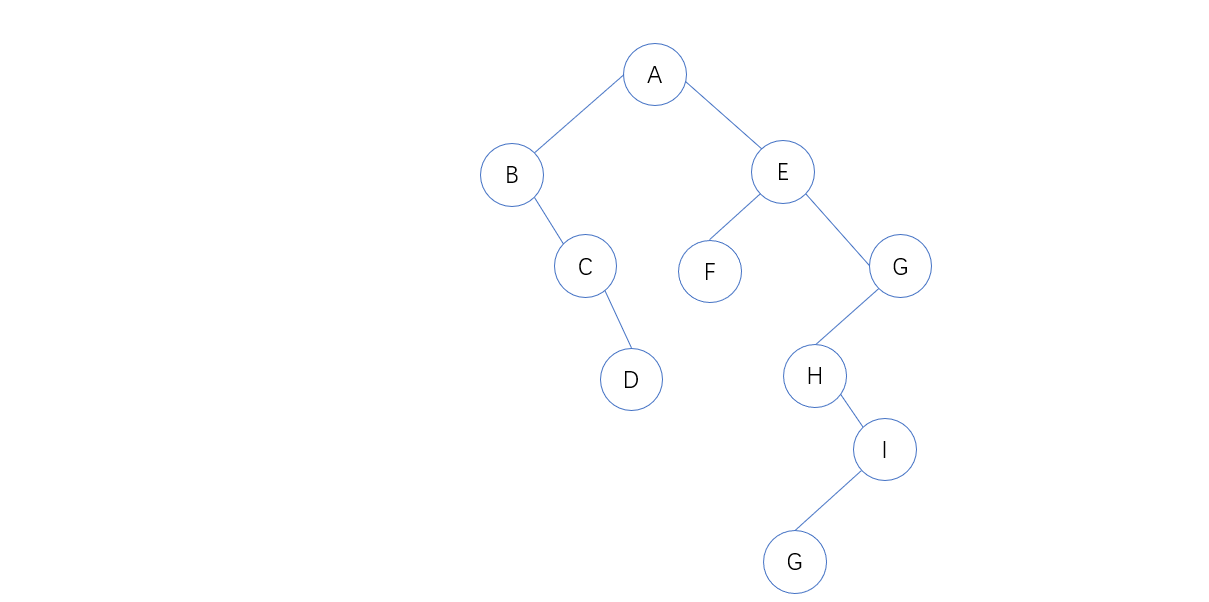
1.  先将森林里的每棵树都利用第二节的方法转为二叉树

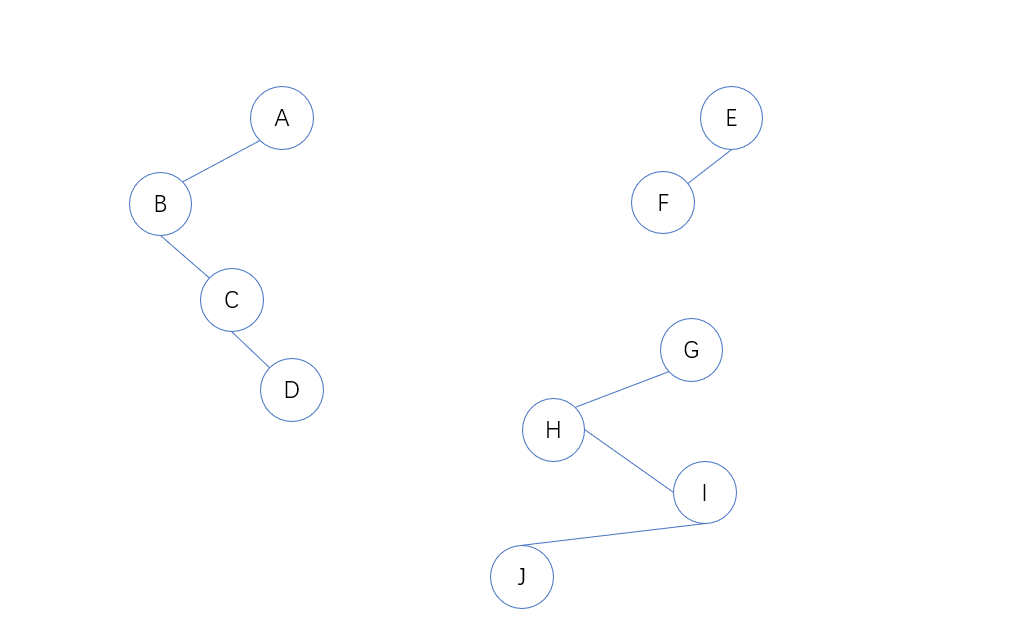
2.  第一棵二叉树不动，从第二课二叉树开始，依次把后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子，依次将所有的二叉树连在一起，转换完成

四.  二叉树转换为树或者森林

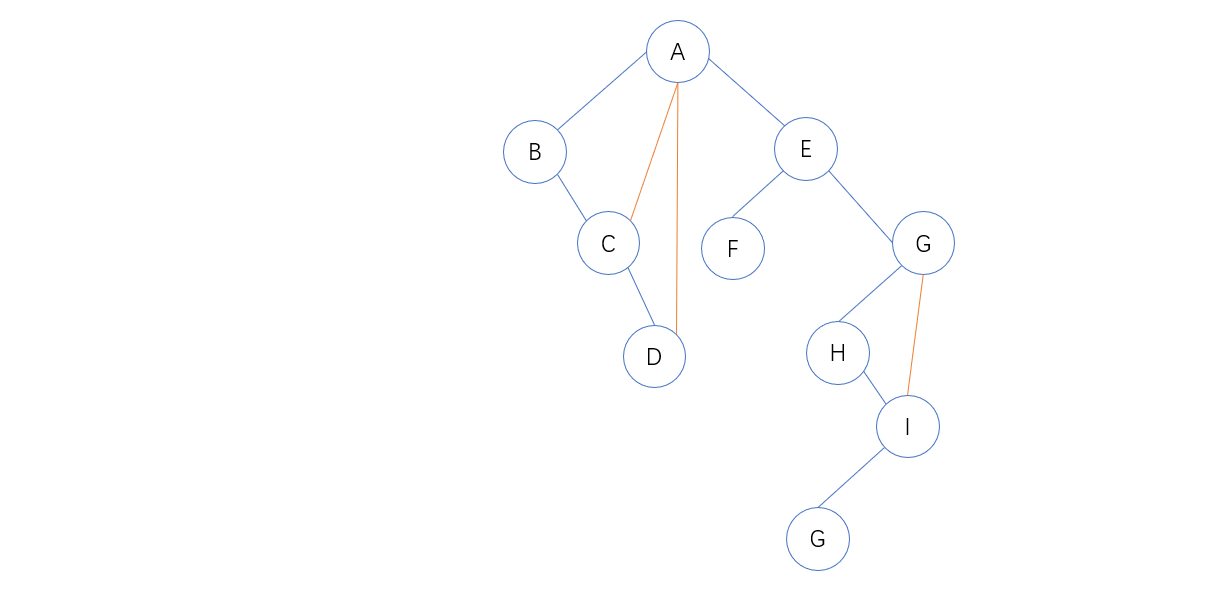
以下图为例：

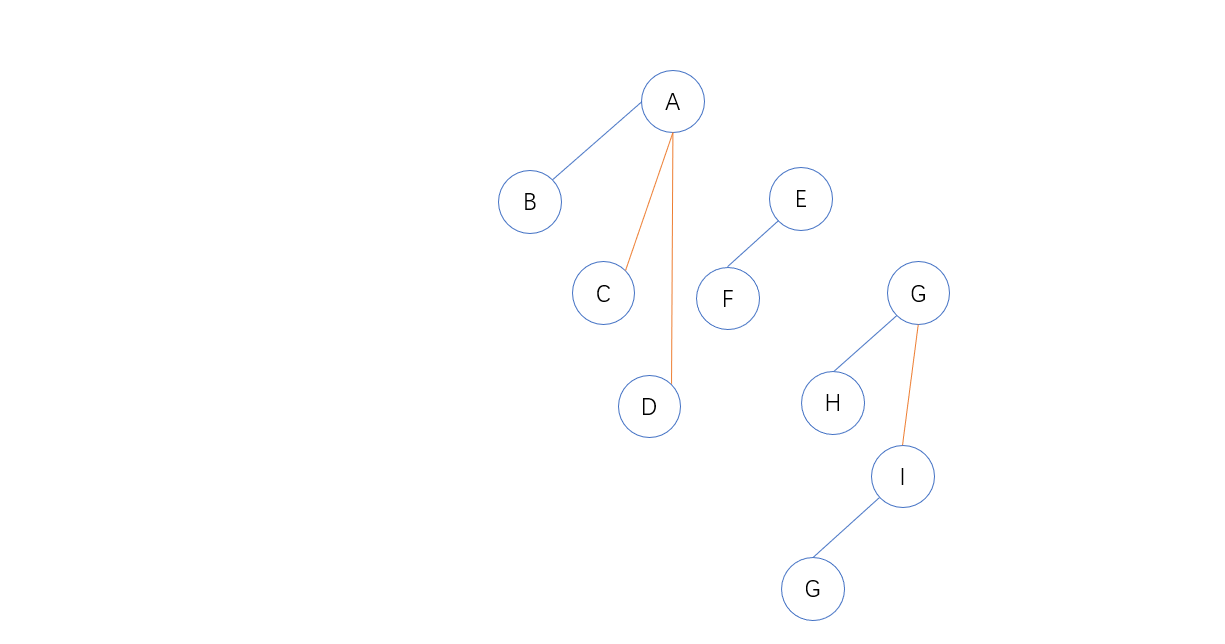
1.  若某结点是其双亲的左孩子，则把该结点的右孩子、右孩子的右孩子……都与该节点的双亲结点连线（下图中红色为该连线）

2.  删掉原二叉树中所有双亲结点和右孩子的连线，转换完成

五.  树和森林的深度优先遍历

树和森林的深度优先遍历又分为：先跟次序遍历和后跟次序遍历

1.  树的先跟次序遍历

遍历顺序为：

1.1  先访问树的根结点

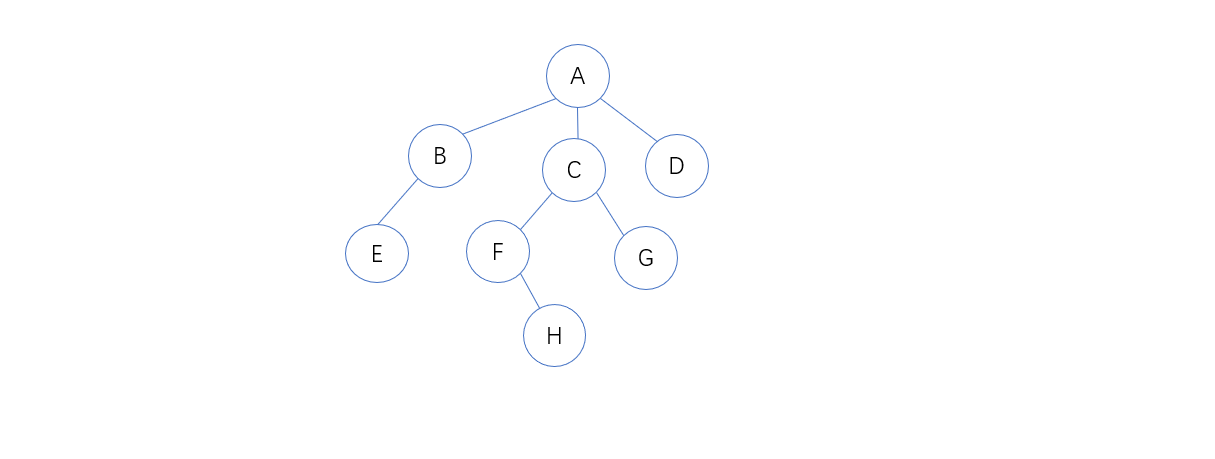
1.2  从左到右，依次先跟遍历根结点的每一棵子树

1.3  上图先跟次序遍历结果为：ABECFHGD

1.4  可以看出前跟遍历和二叉树的前序遍历是一样的

2.  树的后跟次序遍历

遍历顺序为：

1.1  从左到右

1.2  依次后跟遍历根结点的每一棵子树

1.3  访问根结点

1.4  上图后跟次序遍历结果为：EBHFGCDA

1.5  可以看出后跟遍历和二叉树的中序遍历是一样的

3.  森林的先跟次序遍历

遍历顺序为：

1.1  先访问森林第一棵树的根结点

1.2  先跟遍历森林中第一棵树的根结点的子树森林

1.3  先跟遍历森林中除第一棵树外其他树组成的森林

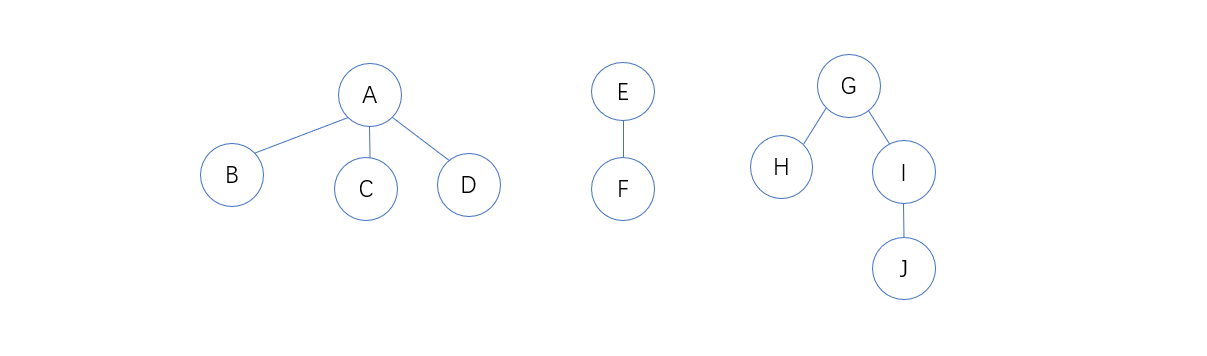
1.4  上图后跟次序遍历结果为：ABCDEFGHIJ

4.  森林的后跟次序遍历

遍历顺序为：

1.1  后跟遍历森林中第一棵树的根结点的子树森林

1.2  访问森林的根结点

1.3  后跟遍历森林中除第一棵树外其他树组成的森林

1.4  上图后跟次序遍历结果为：BCDAFEHJIG

六.  树和森林的广度优先遍历

1.  树的广度优先遍历

树的广度优先遍历就是一层一层的从左向右依次访问，上图遍历顺序为：RABCDEF

2.  森林的广度优先遍历

森林的广度优先遍历就是将所有的书一层一层的对齐，然后一层一层的从左向右依次访问，上图遍历顺序为：AEGBCDFHIJ

参考资料：

西北大学数据结构公开课