张甲49站长

2017-12-03 16:05电脑端

查看作者

最小堆的创建调整插入和删除，以及堆的性质

一. 最小堆和最大堆

1. 关键码

假定在各个数据记录中存一个能够标识数据记录的数据项，并将依据该数据项对数据进行组织，则可称此数据项为关键码（Key）

2. 最小堆

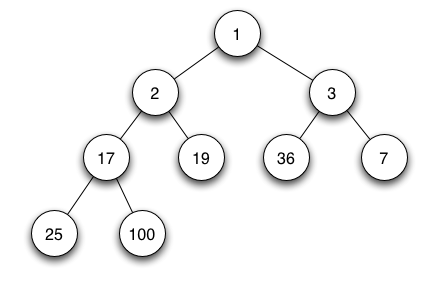
最小堆其中任一非叶节点的数据值均不大于其左子和右子的的数据值，并且根结点的值是最小的

举例：

3. 最大堆

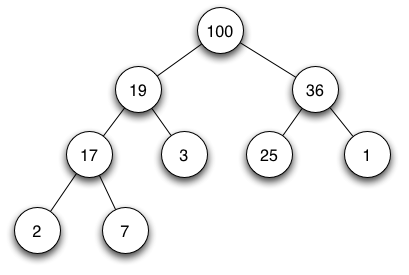
最大堆其中任一非叶节点的数据值均不小于其左子和右子的的数据值，并且根结点的值是最大的

举例：

注意：最小堆和最大堆都是基于完全二叉树的

二. 堆的性质

因为堆存储在下标从0开始计数的数组中，所以在堆中给定下标为i的结点时，有以下性质：

1. 若i = 0，则结点i为根，无父结点；若 i > 0，则结点i的父结点为结点⌊ ((i – 1) / 2) ⌋（ ⌊ 向下取整的意思 ⌋ ）

2. 若2 * i + 1 <= n – 1，则结点i的左子女为结点 2 * i + 1，若2 * i + 1 > n – 1 ，则 i 无左子

3. 若2 * i + 2 <= n – 1，则结点i的右子女为结点2 * i+ 2，2 * i + 2 > n – 1，则i无右子

4. 若结点编号i为奇数，且 i != n – 1，它处于左兄弟位置，则它的右兄弟为结点 i + 1

5. 若结点编号i为偶数，且 i != 0，它处于右兄弟位置，则它的左兄弟为结点 i – 1

6. 结点i所在层次为：⌊ (log2(i + 1) ) ⌋ + 1 （ ⌊ 向下取整的意思 ⌋ ）

7. n个结点的完全二叉树最后一个分支节点下标：⌊（n – 2）/ 2 ⌋

三. 堆的建立

方法一：

通过一个构造函数建立一个空堆，其大小通过动态存储分配得到

方法二：

通过一个构造函数，复制一个记录数组并对其加以调整成一个堆

四. 最小堆的下滑调整

有时候给出一个记录的关键码集合，数据的排列可能不是最小堆的形式，因此需要按照自下向上逐步调整的方法把它调整成为了一个最小堆，步骤如下：

1. 首先通过第二节中性质7获取该堆中最后一个分支节点的下标

2. 然后将该结点和其左子以及右子比较，如果小于左子或者右子，则互换位置

3. 当前分支节点比较完成，再用同样的方法比较其前一个节点

4. 如果当前节点和它的子节点发生了位置交换，则继续判断子节点的下一层（因为下一层的父节点已经变更）

举例：

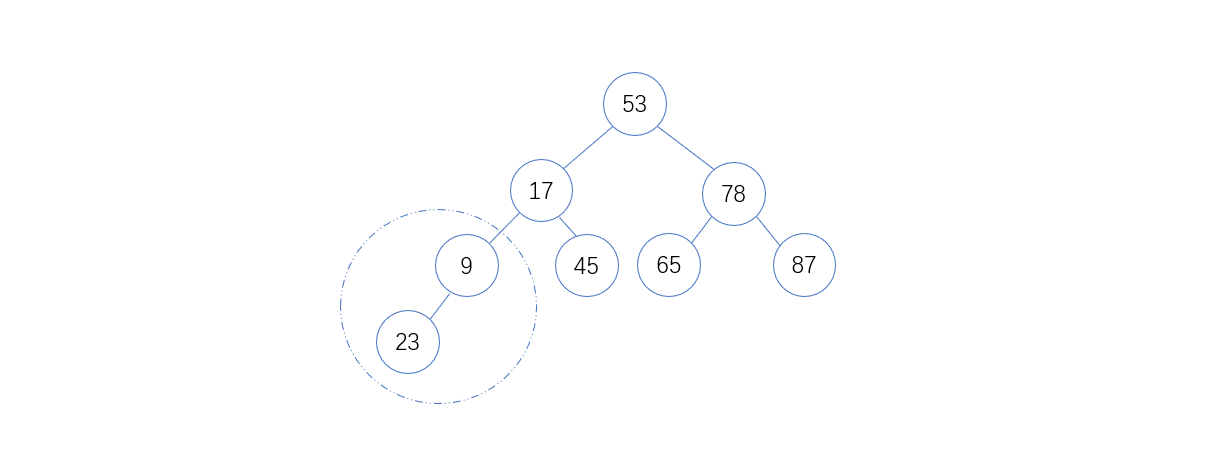
1. 首先，该图有8个结点，则找到最后一个分支节点为（8 – 2）/ 2 = 3，下标为3的元素是9，将9和23比较，9 < 23 ，无需互换，如下图：

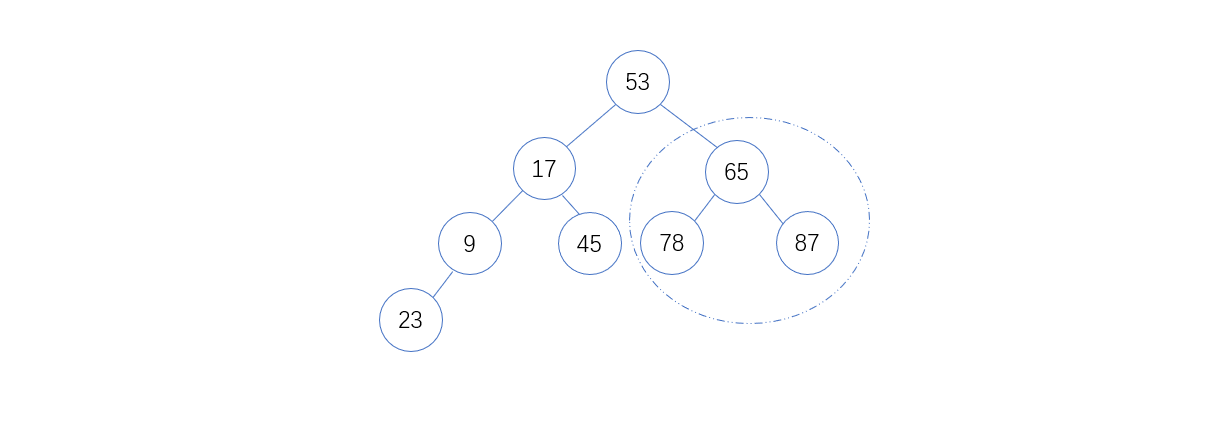
2. 将78和65以及87比较，65 < 78 ,则互换位置后如下图：

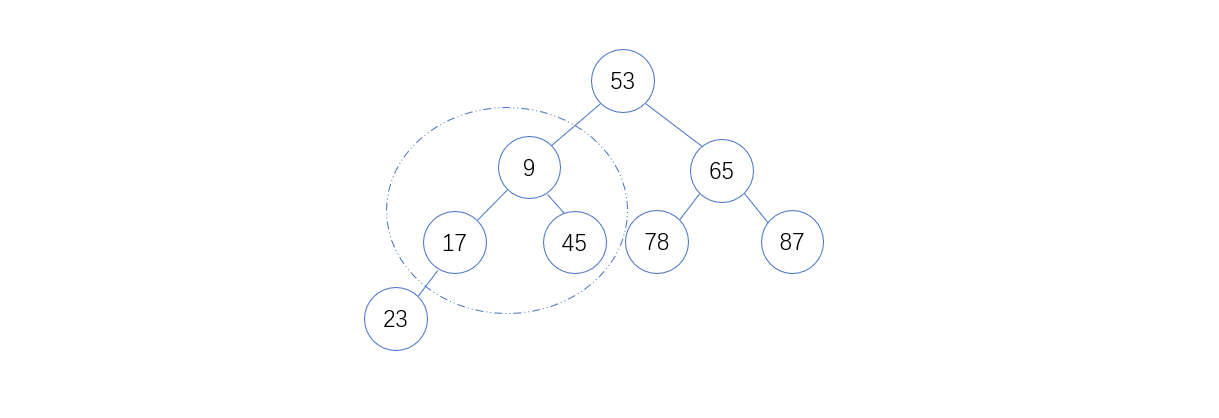
3. 将17和9以及45比较，9 < 17,则互换位置后如下图：

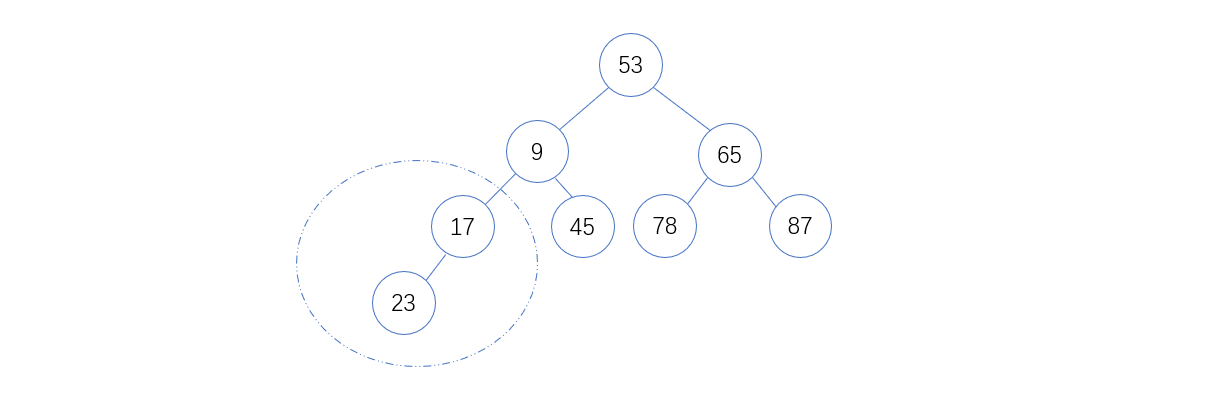
4. 将17和23比较，17 < 23 ,无需互换，如下图：

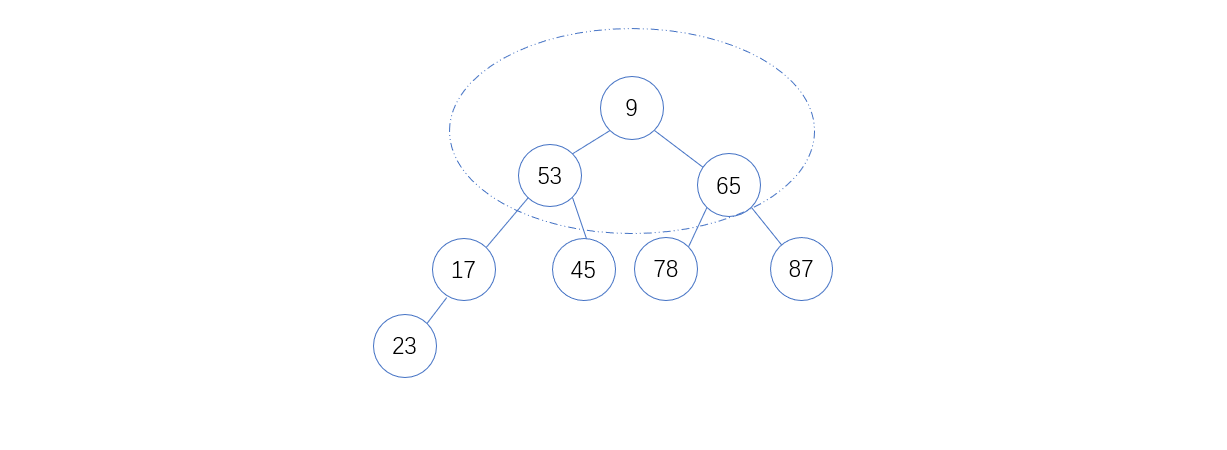
5. 将53和9以及65比较，9 < 53 ,则互换位置后如下图：

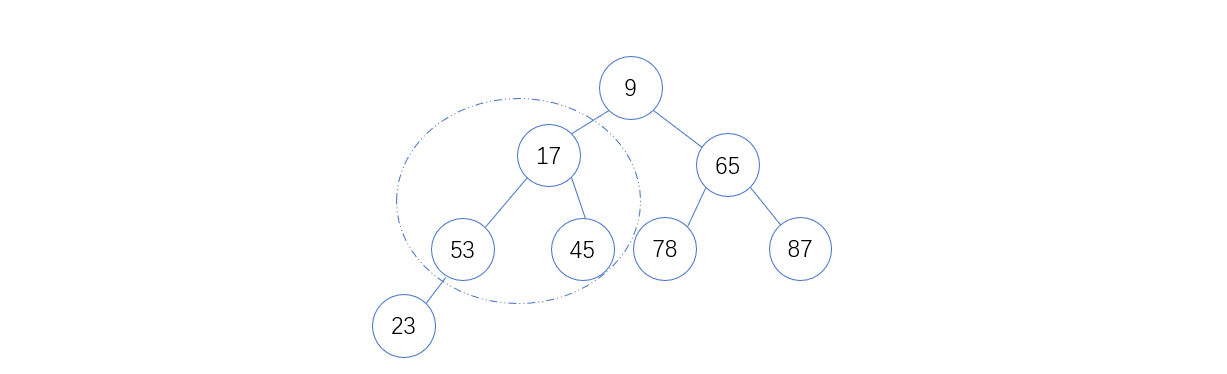
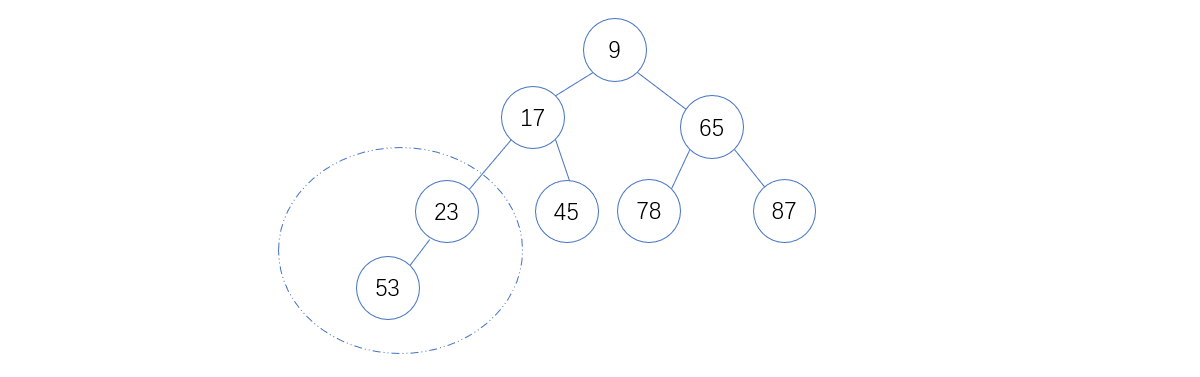
6. 将53和17以及45比较，17 < 53,则互换位置后如下图：

7. 将53和23，53 > 23 ,则互换位置后如下图：调整完成

我们可以发现，只要有结点和其他结点互换了位置，则该节点的子孙结点都需要递归进行调整

五. 堆的插入

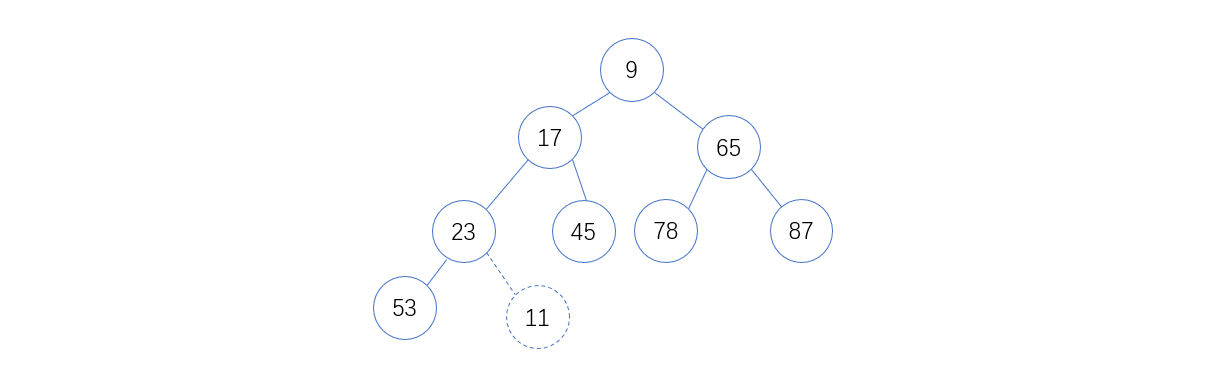
通常，插入都是将新的结点插入到最小堆的最后一个结点后面，然后可以采用自下而上的算法调整成最小堆。比如在下面的最小堆中插入11这个节点

1. 首先将11和23比较，11 < 23 ，则互换位置

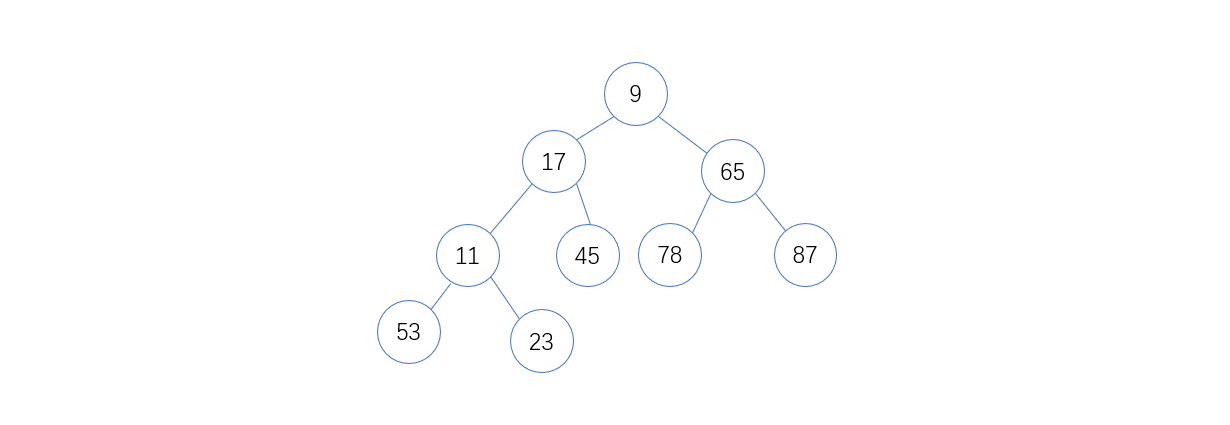
2. 接下来，将11和17比较，再次互换位置

3. 再将11和9比较，11 < 9 ，无需互换，插入完成

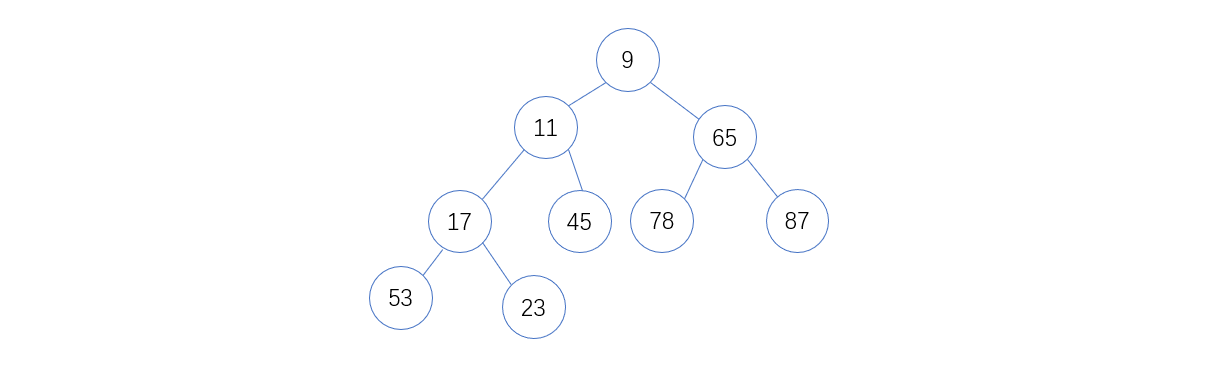
六. 堆的删除

通常，堆的删除是将最小堆的根结点删除，然后将将最小堆的最好一个结点填补根结点的位置，然后将堆的实际元素个数-1，再按照从上向下的算法调整成最小堆

七. 代码实现

#include<stdio.h>
#include<iostream>
using namespace std;
class MinHeap//定义最小堆类
{
private:
    int* data;//存放数据
    int sz;//数组长度
    int cur_sz;//最小堆中当前元素个数
public:
    MinHeap(int arr[], int n);//通过第二种方法，即通过一个数组创建一个最小堆，n代表数组的长度
    void siftDown(int curPos,int maxPos);//从下向上调整成最小堆
    void siftUP(int start);//最小堆的插入算法调用此方法进行自下而上调整成最小堆
    void print();//输出堆中的所有数据
    bool Insert(int x);//插入元素
    bool Remove();//删除根结点
};

MinHeap :: MinHeap(int arr[], int n)
{
    sz =  (10 < n) ? n : 10; //初始化数组长度
    data = new int[n];//分配堆存储空间
    cur_sz = n;//初始化最小堆中当前元素个数
    for(int i = 0; i < n; i++)
    {
        data[i] = arr[i];//复制数组
    }
    int curPos = (n - 2)/ 2;//最后一个分支节点下标
    while(curPos >= 0)// 自底向上 逐步扩大形成堆
    {
        siftDown(curPos,cur_sz - 1);//cur_sz是当前节点个数，-1是最大下标
        curPos--;//向前换一个分支节点
    }
}
void MinHeap :: siftUP(int start)
{
    int j = start;//j为最后一个结点的下标
    int i = (j - 1) / 2;//下标为j的结点的父结点
    int temp = data[j];
    while(j > 0)//沿着父结点向上直达根结点结束
    {
        if(data[i] <= temp) break;
        else
        {
            data[j] = data[i];
            j = i;
            i = (i - 1) / 2;
        }
    }
    data[j] = temp;
}


void MinHeap :: siftDown(int start, int m)
{

    int i = start;
    int j = 2 * i + 1;//i的左子
    int temp = data[i];
    while(j <= m)//判断下标为i的结点的左子有没有左子，是否需要递归调整
    {
        if(j < m && data[j] > data[j + 1])//如果j = m，说明最后一个结点是左结点，就没有与之相对应的右节点比较
            //如果j != m，并且左子大于右子
        {
            j++;//则接下来和右子进行比较
        }
        if(temp < data[j]) break;//如果该节点小于右子，则无需交换值，直接跳出循环
        data[i] = data[j];
        i = j;
        j = 2 * i + 1;
    }
    data[i] = temp;
}

/*
void MinHeap :: siftDown(int start, int m)
{
    int i = start;
    int j = 2 * i + 1;
    int temp = 0;
    while(j <= m)
    {
        if(j < m && data[j] > data[j + 1])
        {
            j++;
        }
        if(data[i] < data[j])
        {
            break;
        }
        else
        {
            temp = data[i];
            data[i]= data[j];
            data[j] = temp;
        }
         i = j;
         j = 2 * i + 1;
    }
}
*/

bool MinHeap :: Insert(int x)
{
    if(cur_sz == sz)
    {
        cout << "堆满了"<< endl;
        return false;
    }
    else
    {
        data[cur_sz] = x;//将插入的结点X存入最小堆的最后面
        siftUP(cur_sz);//调用siftUP算法，实现自下而上调整成最小堆
        cur_sz++;//插入完成，将最小堆中当前元素个数 + 1
        cout << "插入" << x << "成功" << endl;
        return true;
    }
}

bool MinHeap :: Remove()
{
    if(!cur_sz)
    {
        cout<< "堆空啦"<< endl;
        return false;
    }
    data[0] = data[cur_sz - 1];//将最小堆的最后一个结点填补取走的根结点
    cur_sz--;
    siftDown(0,cur_sz - 1);
    cout << "已经删除根结点"<< endl;
}
void MinHeap :: print()
{
    for(int i = 0; i < cur_sz; i++)
    {
        printf("%d \n", data[i]);
    }
}

int main()
{

    int a[] = {53,17,78,9,45,65,87,23};

    MinHeap mh(a,8);
    mh.print();
    cout << "---------------------" << endl;
    mh.Insert(11);
    cout << "---------------------" << endl;
    mh.print();
    cout << "---------------------" << endl;
    mh.Remove();
    mh.print();
    return 0;
}
输出：
9
17
65
23
45
78
87
53
---------------------
插入11成功
---------------------
9
11
65
17
45
78
87
53
23
---------------------
已经删除根结点
11
17
65
23
45
78
87
53