一. 前言
在本周,数据结构和离散数学几乎同时学到了Huffman算法,两个老师都对该算法大加称赞,特别是知道该算法可以用于无损数据压缩的熵编码(权编码)后,自己便更加的感兴趣,将相关知识整理如下
二. Huffman简介
在了解Huffman算法前,我们先来了解一下Huffman树:Huffman树,又称最优二叉树,是一类加权路径长度最短的二叉树,给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近
三. 树的路径长度
在将Huffman树之前,我们先引入路径和路径长度的概念
1. 路径
从树中一个结点到另一个节点之间的的分支构成该两结点之间的路径,从树的根结点到达树中每一个结点有且仅有一条路径
2. 路径长度
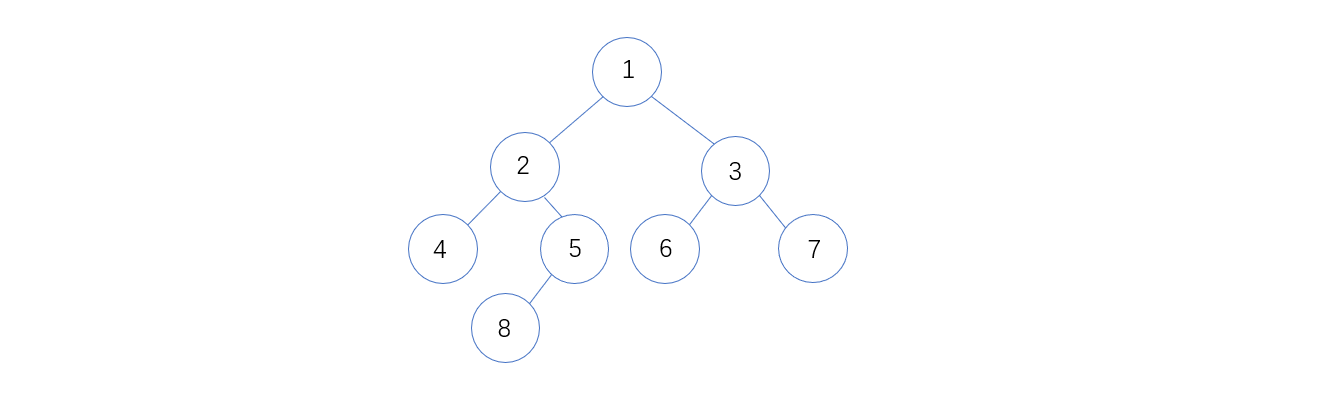
指路径上的分支条数,树的路径长度(PL)是从树的根结点到每一个结点的路径长度之和,且从根结点到其他各个结点的路径长度等于该结点所在层次 k – 1,比如下图:
1 到 1 的路径长度为0,1 到 2 的路径长度为1
1 到 3 的路径长度为1,1 到 4 的路径长度为2
1 到 5 的路径长度为2,1 到 6 的路径长度为2
1 到 7 的路径长度为2,1 到 8 的路径长度为3
则树的路径长度PL为:0+1+1+1+2+2+2+2+3 = 14
同时我们可以看成,第 i 层的结点个数最多有2^(i – 1)个,而第 i 层结点到根结点路径长度为i – 1,所以到根结点的路径长度为k的结点最多有2^k个
四. Huffman树
11. 带权路径长度
将一个有n个权值的集合{ω1,ω2,ω3……ωn}(ωi >=0,1 <= i <= n)分别赋给一棵具有n个叶结点的二叉树T的每一个叶节点,则称T是权值为ω1,ω2,ω3……ωn的扩充二叉树,带有权值的叶节点叫做扩充二叉树的外结点,其余的不带权值的分支节点叫做内结点
同时,外结点的带权路径长度(WPL) = T的根到该节点的路径长度 * 该节点的权值
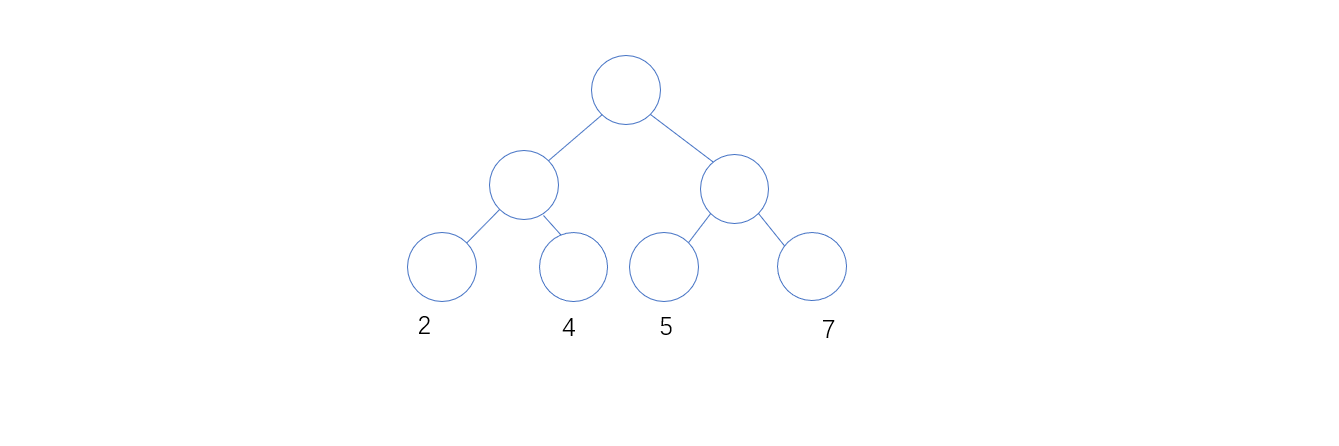
举例:
WPL = 2 * 2 + 4 * 2 + 5 * 2 + 7 * 2 = 36
另外值得注意的是:带权路径长度最小的扩充二叉树不一定是完全二叉树,而是权值大的外结点离根结点最近的扩充二叉树,这就是Huffman树
五. Huffman算法
为了构造权值集合为{ω1,ω2,ω3……ωn}的Huffman树,Huffman提出了一个构造算法,称之为:Huffman算法,步骤如下:
1. 作n个叶节点,分别以ω1,ω2,ω3……ωn为权
2. 从所有入度为0的结点中,选出两个权最小的顶点,分别以左子、右子树组成一个新的分支节点代替左、右子树比较
3. 重复第2步,直到只有一个入度为0的顶点为止
举例:
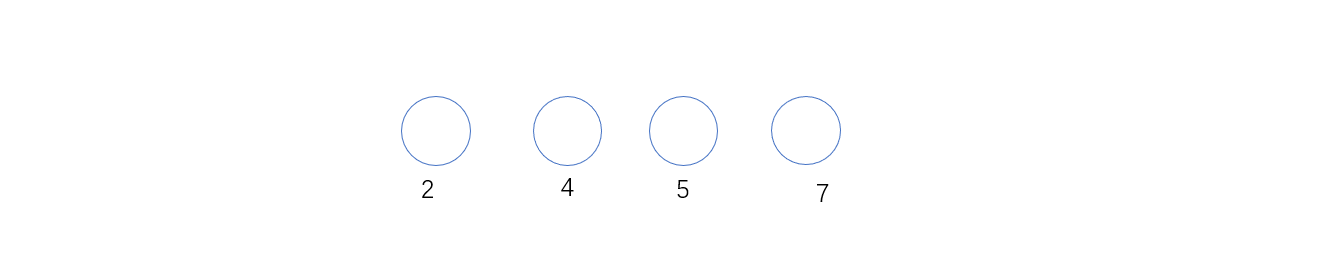
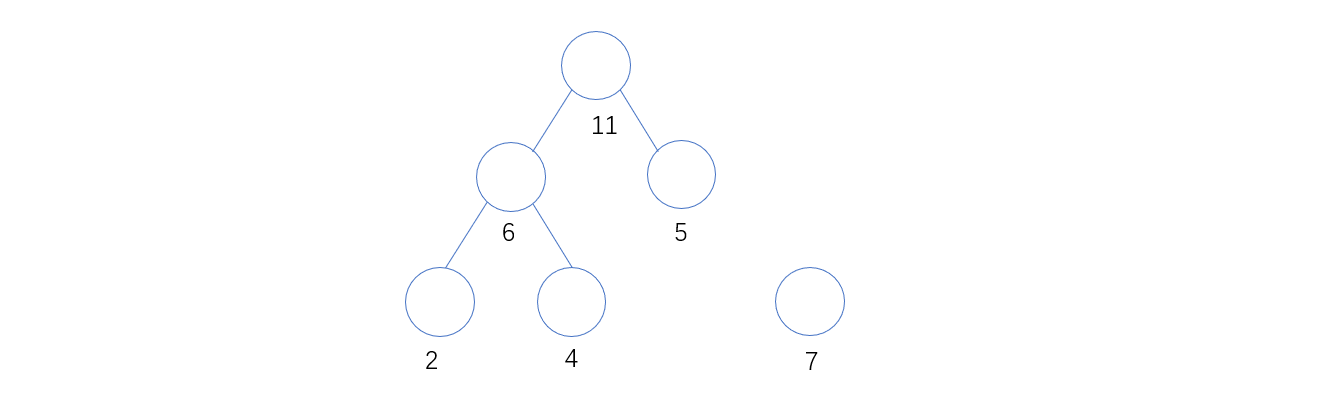
1. 作4个叶节点,分别以2,4,5,7为权
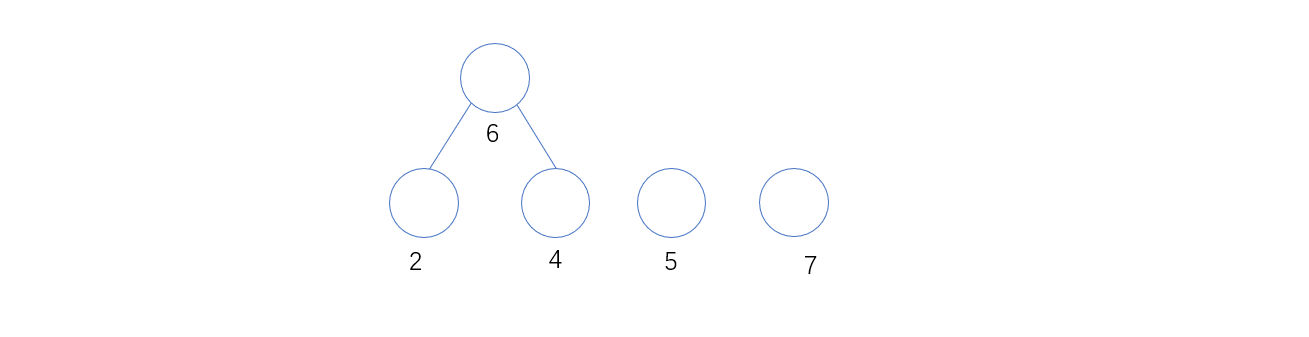
2. 从所有入度为0的结点中,最小的两个结点为2和4,则组成6这个分支节点
3. 从所有入度为0的结点中,最小的两个结点为5和6,则组成11这个分支节点
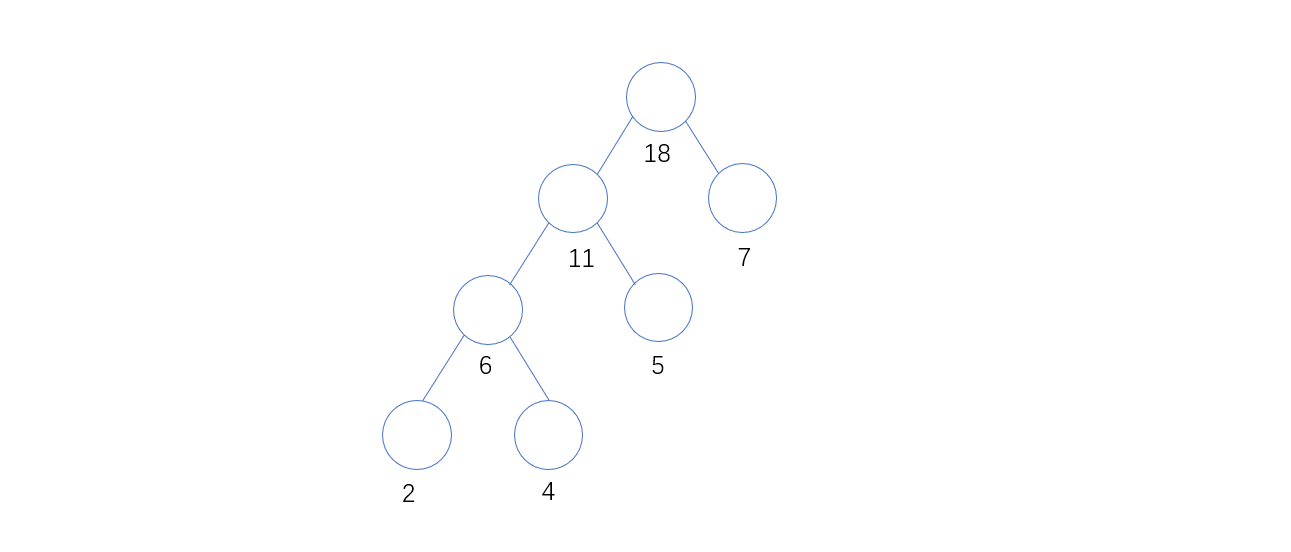
4. 从所有入度为0的结点中,最小的两个结点为7和11,则组成18这个分支节点,此时只有一个入度为0的顶点为18,组成了下图的二叉树,完成
值得注意的是:由于每一步选择最小权的选法不唯一,所以通过该算法画出的二叉树形状也不唯一,但是WPL都应该是一样的
六. 代码实现
《数据结构》殷人昆版的Huffman算法是用最小堆实现的,而《数据结构》严蔚敏版是用多个数组实现的,这里以严蔚敏版为例(因为这个更好理解一些,方便没有学好最小堆的同学理解Huffman)
思路:
由于Huffman树中没有度为1的结点,所以一棵有n个叶节点的Huffman树又2n-1个结点,可以存储在一个大小为2n – 1 的一维数组中,首先,我们需要以下几个数组(以权值集合{8,4,5,2}为例):
11. 一个用于存放树中每个节点值的数组,最后结果如下图:
2. 一个用于存放树中每个节点的父结点下标的数组,最后结果如下图:
3. 一个用于检测每个节点入度是否为0的数组(即有没有被使用),最后结果如下图:
4. 一个用于检测每个结点是左子树还是右子树的数组(注意这里结果不唯一,因为部分结点即可作为左子,又可以作为右子)
代码实现:
#include<stdio.h>
void huffman(int w[],int n) //w 权重数组,n是数组的长度
{
// 创建数组
int* t = new int [2 * n - 1];//存储树节点的值
int* parent = new int [2 * n - 1];//存储树的节点的父节点的下标,默认值-1
int* flag = new int [2 * n - 1];//是否已被使用,0未被使用,1被使用
int* lor = new int [2 * n - 1];//判断是左子树还是右子树,默认-1,0为左,1为右,-1为根结点
int m = 2 * n - 1;
//初始化四个数组
int i = 0;
int j = 0;
for(i = 0; i < m; i++)
{
t[i] = 0;
parent[i] = -1;
flag[i] = 0;
lor[i] = -1;
}
for( i = 0; i < n; i++)
{
t[i] = w[i];
}
int p,q;//最小值的下标
for( i = 0; i < n - 1; i++) //执行n - 1 次
{
p = -1, q = -1;
//找到最小的
for( j = 0; j < n + i; j++)
{
if(flag[j] == 1) continue;//跳过已经使用过的节点
if(p == -1) p = j;
else if(t[j] < t[p])
{
p = j;
}
}
flag[p] = 1;
lor[p] = 0;
//找第二小的
for(j = 0; j < n + i; j++)
{
if(flag[j] == 1)continue;//跳过已经使用的节点
if(q == -1) q = j;
else if (t[j] < t[q])
{
q = j;
}
}
flag[q] = 1;
lor[q] = 1;
//合并
t[n+i] = t[p] +t[q];
parent[p] = n + i;
parent[q] = n + i;
}
printf("w = ");
for (i= 0; i< m; i++)
{
printf("%4d ",t[i]);
}
printf("\n");
printf("lor = ");
for (i= 0; i< m; i++)
{
printf("%4d ",lor[i]);
}
printf("\n");
printf("parent = ");
for(i =0; i<m; i++)
{
printf("%4d ",parent[i]);
}
printf("\n");
printf("flag = ");
for(i = 0; i<m; i++)
{
printf("%4d ",flag[i]);
}
printf("\n");
}
int main()
{
int w[] = {8,4,5,2};
huffman(w,4);
return 0;
}
输出:
w = 8 4 5 2 6 11 19
lor = 0 1 0 0 1 1 -1
parent = 6 4 5 4 5 6 -1
flag = 1 1 1 1 1 1 0
ps. 关于Huffman 编码请查看本文:Huffman






请登录之后再进行评论