一. Huffman编码简介
霍夫曼编码(英语:Huffman Coding),又译为哈夫曼编码、赫夫曼编码,是一种用于无损数据压缩的熵编码(权编码)算法。由大卫·霍夫曼在1952年发明。在计算机数据处理中,霍夫曼编码使用变长编码表对源符号(如文件中的一个字母)进行编码,其中变长编码表是通过一种评估来源符号出现机率的方法得到的,出现机率高的字母使用较短的编码,反之出现机率低的则使用较长的编码,这便使编码之后的字符串的平均长度、期望值降低,从而达到无损压缩数据的目的。——————摘自维基百科
二. 哈夫曼算法应用
假设我们需要传送的电文为ABACCDA,它由四个字符:ABCD重复组合而成,我们可以假设A、B、C、D的编码分别为00、01、10和11,(最低是2位,如果是1位,只能表示2个)则上述7个字符的电文便为00010010101100,总长14位
当然,在传送电文时,我们希望传输的总长越短越好。如果对每个字符设计长度不等的编码,且让电文中出现次数较多的字符采用尽可能短的编码,则传送电文的总长便可减少。如果设计A、B、C、D的编码分别为0、00、1和01,则上述7个字符的电文可转换成总长为9的字符串000011010。但是这样的电文无法还原,因为前4个字符的子串0000就可有多种译法:AAAA、ABA,BB等,因此,我们引出前缀码的概念
三. 前缀码
我们设计长短不等的编码,必须是任一个字符的编码都不是另一个字符的编码的前缀,这种编码称做前缀编码
比如{1,00,011,0101,01001,01000}就是一个前缀码,而{1,00,011,0101,01011,01000} 就不是前缀码,因为0101是01011的前缀
四. 二元前缀码
由0和1组成的前缀码称作二元前缀码
五. 最优前缀码
由Huffman树产生的前缀码成为最优前缀码,下面介绍如何用Huffman树产生前缀码
将二叉树的叶节点标记字符,由根结点沿着二叉树路径下行,每个分支点引出的左边标0,右边标1,则每条从根结点到叶节点的路径唯一表示了该叶节点的二元前缀码,如下图:
六. Huffman算法应用
我们给出以下字符:{'a','b','a','a','c','d','a','b','a','b','a','a','b','c','d','c','a','a','b','a'}
a:出现10次
b:出现5次
c:出现3次
d:出现2次
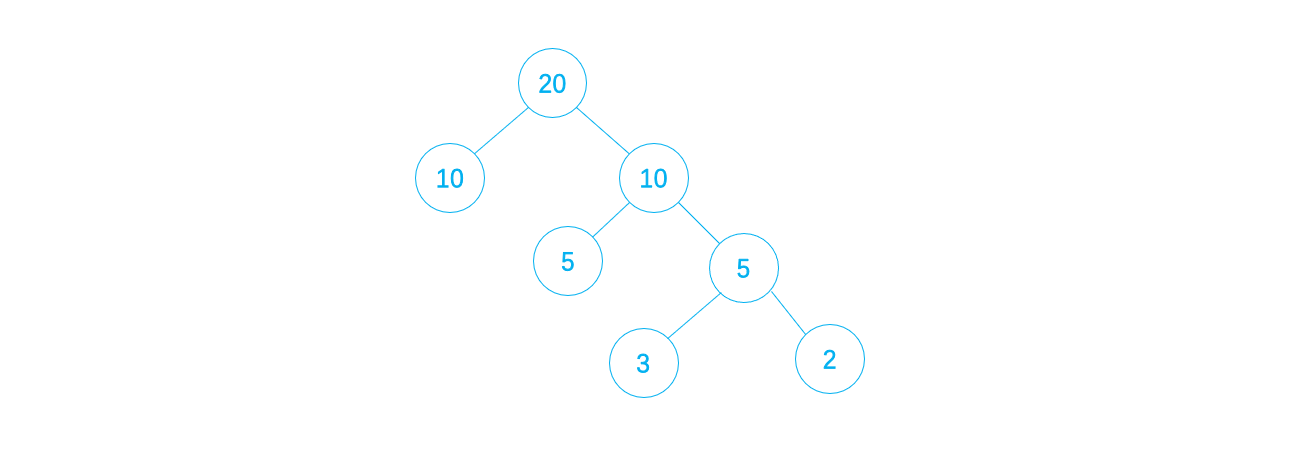
则权值集合为{10,5,3,2},根据Huffman算法构造二叉树如下:
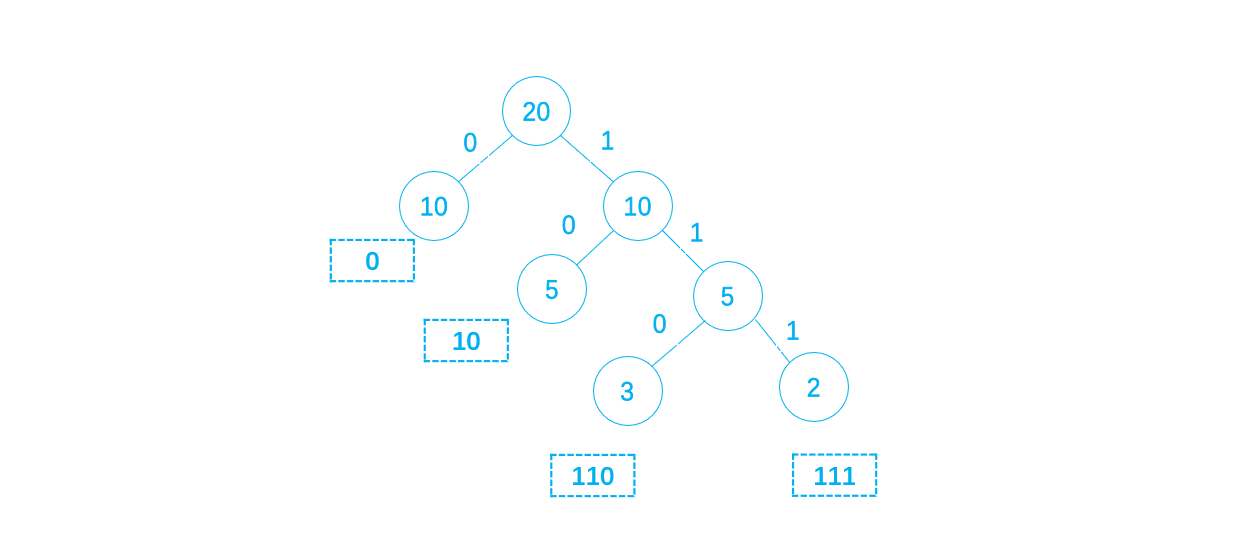
对该Huffman树进行编码,如下:
则:0传a,10传b,110传c,111传d,则原序列用编码的序列表示为:
01000 11011 10100 10001 01101 11110 00100
WPL = 10 *1 + 5 * 2 + 3 * 3 + 2 * 3 = 35
,而如果用2个长度传输这些字符,需要 2 * 20 = 40个字符。总结如下:
1. 统计每个字符的出现频率
2. 将出现频率作为权值集合,根据Huffman算法构造Huffman树
3. 对Huffman树进行编码
4. 把原序列变成编码的序列
5. 统计WPL
七. 代码实现
#include<stdio.h>
void huffman(int w[],int n) //w 权重数组,n是数组的长度
{
// 创建数组
int* t = new int [2 * n - 1];//存储树节点的值
int* parent = new int [2 * n - 1];//存储树的节点的父节点的下标,默认值-1
int* flag = new int [2 * n - 1];//是否已被使用,0未被使用,1被使用
int* lor = new int [2 * n - 1];//判断是左子树还是右子树,默认-1,0为左,1为右,-1为根结点
int* HuffmanCode = new int [9];
int m = 2 * n - 1;
int x = m ;
//初始化四个数组
int i = 0;
int j = 0;
for(i = 0; i < m; i++)
{
t[i] = 0;
parent[i] = -1;
flag[i] = 0;
lor[i] = -1;
}
for( i = 0; i < n; i++)
{
t[i] = w[i];
}
int p,q;//最小值的下标
for( i = 0; i < n - 1; i++) //执行n - 1 次
{
p = -1, q = -1;
//找到最小的
for( j = 0; j < n + i; j++)
{
if(flag[j] == 1) continue;//跳过已经使用过的节点
if(p == -1) p = j;
else if(t[j] < t[p])
{
p = j;
}
}
flag[p] = 1;
lor[p] = 0;
//找第二小的
for(j = 0; j < n + i; j++)
{
if(flag[j] == 1)continue;//跳过已经使用的节点
if(q == -1) q = j;
else if (t[j] < t[q])
{
q = j;
}
}
flag[q] = 1;
lor[q] = 1;
//合并
t[n+i] = t[p] +t[q];
parent[p] = n + i;
parent[q] = n + i;
//printf("lor2 == %d\n",lor[p]);
//printf("x1 == %d\n",sub[p]);
}
/*
int s = 0;
for( i = 0; i < 4; i++)
{
int k = m - parent[i] - 1;//
//K1=7-6-1=0
//k2 = 7-4-1=2;
//k3 =7-5-1=1;
//k4 = 7-4-1 = 2
int r = 0;
for( int r = 0; r < k ; r++)
{
HuffmanCode[s] = lor[parent[i]];
// printf("hu =%d,s = %d\n",HuffmanCode[s],s);
s++;
}
HuffmanCode[s] = lor[i];
//printf("hu2 =%d,s = %d\n",HuffmanCode[s],s);
s++;
}
*/
int k,s = 0;
for(i = 0; i < n; i++)
{
k = i;
HuffmanCode[s] = lor[i];
s++;
while(lor[parent[k]]!= -1)
{
HuffmanCode[s] = lor[parent[k]];
k = parent[k];
s++;
}
}
printf("Hm = ");
for (i= 0; i < 9; i++)
{
printf("%4d",HuffmanCode[i]);
}
printf("\n");
int u = 8;
for(i = n - 1; i >= 0; i--)
{
printf("%d的编码是:",t[i]);
int t = m - parent[i];
for(j = 0; j < t; j++)
{
printf("%d",HuffmanCode[u]);
u--;
}
printf("\n");
}
printf("w = ");
for (i= 0; i< m; i++)
{
printf("%4d ",t[i]);
}
printf("\n");
printf("lor = ");
for (i= 0; i< m; i++)
{
printf("%4d ",lor[i]);
}
printf("\n");
printf("parent = ");
for(i =0; i<m; i++)
{
printf("%4d ",parent[i]);
}
printf("\n");
printf("flag = ");
for(i = 0; i<m; i++)
{
printf("%4d ",flag[i]);
}
printf("\n");
}
int main()
{
int w[] = {8,4,5,2};
huffman(w,4);
return 0;
}
//8,4,5,2,分别对应0 111 101 10
输出:
Hm = 0 1 1 1 0 1 0 1 1
2的编码是:110
5的编码是:10
4的编码是:111
8的编码是:0
w = 8 4 5 2 6 11 19
lor = 0 1 0 0 1 1 -1
parent = 6 4 5 4 5 6 -1
flag = 1 1 1 1 1 1 0
2017-12-11 更新记录:
在@XP的帮助下,发现了之前的算法无法输出左右左的情况,已经修复,并且添加了还原功能
八. 参考资料
《数据结构》严蔚敏版



请登录之后再进行评论