散列方法和散列函数

一. 散列表和散列方法

问：什么是散列方法？
答：我们可以在元素存储位置与其关键码之间建立一个确定的对应函数关系Hash()，使得每个关键码与结构中一个唯一的存储位置相对应，即Address ＝ Hash(key)，在插入时依此函数计算存储位置并按此位置存放。在搜索时对元素的关键码进行同样的计算，把求得的函数值当做元素存储位置，在结构中按此位置搜索。这就是散列方法

二. 散列函数

问：什么是散列函数？

答：在散列方法中使用的转换方法叫做散列函数，按照这个想法构造出来的表或者结构叫做散列表

问：那么我们在构造散列函数的时候，有哪些注意事项呢？

答：主要需要注意以下几点：

散列函数应是简单的，能在较短的时间内计算出结果。
散列函数的定义域必须包括需要存储的全部关键码，如果散列表允许有 m 个地址时，其值域必须在 0 到 m-1 之间。
散列函数计算出来的地址应能均匀分布在整个地址空间中 : 若 key 是从关键码集合中随机抽取的一个关键码, 散列函数应能以同等概率取0 到 m-1 中的每一个值。

散列函数常用的有四种：除留余数法、数字分析法、平方取中法、折叠法：

1. 除留余数法

设散列表中允许地址数为m，取一个不大于 m，但最接近于或等于 m 的质数 p 作为除数，用以下函数把关键码转换成散列地址：

hash (key) = key % p p <= m的质数

其中，“%”是整数除法取余的运算，要求这时的质数 p 不是接近 2 的幂。

举例: 有一个关键码 key = 962148，散列表大小 m = 25，即 HT[25]。取质数 p = 23。散列函数 hash(key) = key % p。则散列地址为

hash(962148) = 962148 % 23 = 12。

可按计算出的地址存放记录。注意, 使用散列函数计算出的地址范围是 0 到 22，而 23、24 这几个地址实际上不能用散列函数计算出来，只能在处理冲突时达到这些地址。

2. 数字分析法

设有 n 个 d 位数, 每一位可能有 r 种不同的符号。这 r 种不同的符号在各位上出现的频率不一定相同。可根据散列表的大小, 选取其中各种符号分布均匀的若干位作为散列地址。数字分析法仅适用于事先明确知道表中所有关键码每一位数值的分布情况，它完全依赖于关键码集合。如果换一个关键码集合，选择哪几位要重新决定。

举例如下：

3. 平方取中法

此方法在词典处理中使用十分广泛。它先计算构成关键码的标识符的内码的平方, 然后按照散列表的大小取中间的若干位作为散列地址。

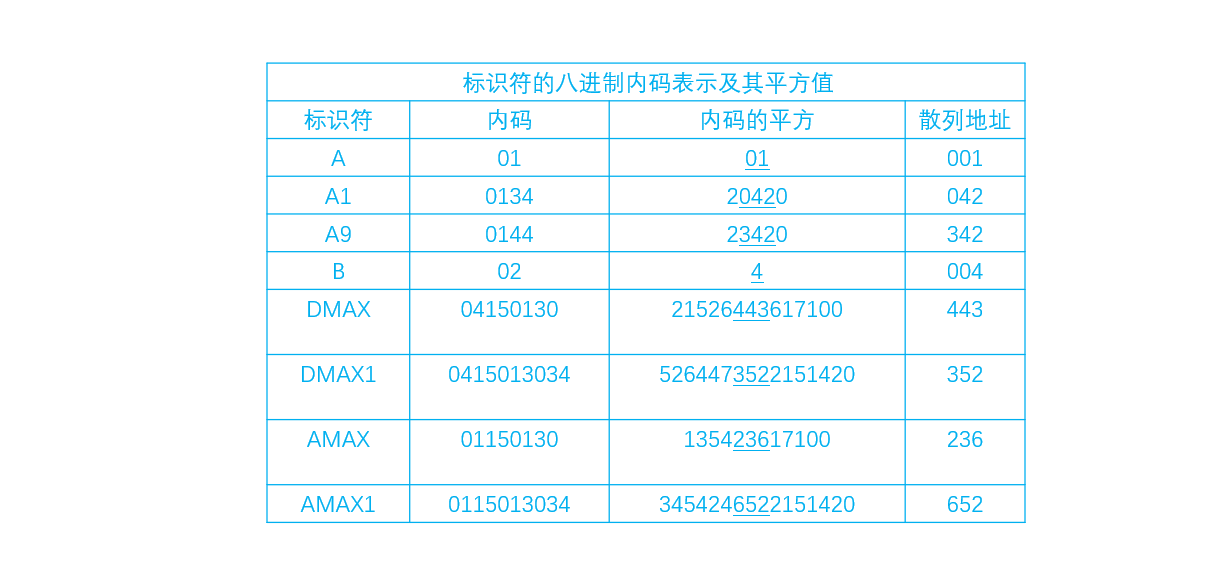
设标识符可以用一个计算机字长的内码表示。因为内码平方数的中间几位一般是由标识符所有字符决定, 所以对不同的标识符计算出的散列地址大多不相同, 即使其中有些字符相同。在平方取中法中, 一般取散列地址为 2 的某次幂。例如, 若散列地址总数取为 m = 2r，则对内码的平方数取中间的 r 位。如果 r = 3，所取得的散列地址参看图的最右一列。

举例：