一. 基本概念
1. 查找表:由具有同一类型的数据元素(或记录)组成的集合称为查找表。
2. 关键字: 关键字是记录中某个项或组合项的值,用它可以标识一个记录。能唯一确定一个记录的关键字,称为主关键字;而不能唯一确定一个记录的关键字,称为次关键字.
3. 查找是指按给定的某个值k,在查找表中查找关键字为给定值k的记录。
4. 查找是计算机中经常遇到的操作。特别是当问题所涉及到的数据量相当大时,查找的效率就显得格外重要。
5. 查找运算的主要操作是关键字的比较,所以,通常把查找过程中对关键字需要执行的平均比较次数(也称为平均查找长度)作为衡量一个查找算法效率优劣的标准。
6. 查找结果有两种:成功或者失败
7. 查找算法的性能指标:时间复杂性、平均查找长度、 平均比较次数
8. 平均查找长度是指为确定对象在搜索表中的位置所执行的关键码比较次数的期望值,对于一个而含有n个对象的表,搜索成功时的平均搜索长度如下图:
二. 顺序查找
1. 无监视哨的顺序查找算法
代码如下:
intSeqSearch(Record r[], intn, intk)
{
int i = 0;
while (i < n && r[i].key != k)i++;
if (i < n) return i;
else return -1;
}
2. 有监视哨的顺序查找算法
代码如下:
int SeqSearch2(Record r[], int n, int k)
{
int i = 0;
r[n].key = k;
while (r[i].key != k) i++;
if (i < n) return i;
else return -1;
}
可以看出,和无监视哨的顺序查找算法相比,while语句少了一个i < n 的判断条件,直接将效率提高了两倍,但是有监视哨会多占用一个存储的空间
3. 顺序查找的平均搜索长度
对于顺序搜素,搜索到第i个对象(i= 0,1…,n-1)需要比较i + 1次,因此ci = i + 1,假设每个兑现的搜索概率都相等,即Pi= 1 / n,则ASLsucc = 1/n * (n * (n + 1) / 2) = ( n + 1 ) /2
三. 二分查找算法
- 二分查找又称为折半查找。
- 二分查找要求顺序表是有序的。
- 二分查找的基本思想是:首先将待查的K值与有序表R[0]到R[n-1]的中间位置mid上的结点的关键字进行比较,若相等,则查找完成;否则,若R[mid].key>K,则说明待查找的结点只可能在左子表R[0]到R[mid-1]中,只需在左子表中继续查找;否则在右子表R[mid+1]到R[n-1]中继续查找。这样,经过一次关键字的比较就缩小了一半的查找区间。如此进行下去,直到找到为止(当然也存在最后找不到的可能)
- 虽然二分查找的效率较高,但它要求被查找序列事先按关键字排好序,而排序本身是一种很费时的运算;另外,二分查找只适用于顺序存储结构,因此,二分查找特别适用于那种一经建立就很少改动、而又需要经常查找的线性表。
- 二分查找的算法复杂度为:O(log n)
1. 非递归版代码
int BiSearch(Record r[ ], int n, int k)
{
low = 0,high = n - 1;
while (low <= high)
{
int mid =(low + high) / 2;
if (r[mid].key == k) return mid;
else if (r[mid].key < k) low = mid + 1;
else high = mid - 1;
}
return -1;
}
2. 递归版代码
int BiSearch2(Record r[], int low, int high, int k)
{
if (low > high)
return -1;
else
{
int mid = (low + high) / 2;
if (r[mid].key == k) return mid;
else if (r[mid].key < k)
return BiSearch2(r,mid + 1,high,k);
else return BiSearch2(r,low,mid - 1,k);
}
}
3. 利用二分查找判定树计算ASL
3.1 如果把当前查找位置上的结点作为根,左子表和右子表的结点分别作为根的左子树和右子树,由此得到的二叉树称为描述二分查找的判定树。
3.2 借助于判定树很容易求得二分查找的平均查找长度。查找数据的比较次数最多为该判定树的树高.
3.3 即在最坏情况下,二分查找方法查找成功的比较次数不超过判定树的高度。
4. C++实现
#include <stdio.h>
struct Stu
{
int id;
char name[20];
int height;
int weight;
};
typedef struct Stu Stu;
//二分查找
int binSearch(Stu s[],int n,int k)
{
int low = 0,high = n-1;
while(low <= high)
{
int mid = (low +high)/2;
if(s[mid].id == k) return mid;
if(k< s[mid].id)
{
high = mid -1;
}
else
{
low = mid +1;
}
}
return -1;
}
//顺序查找
int seqSearch(Stu s[], int n, int k)
{
int i=0;
while (i < n && s[i].id != k) i++;
if (i<n) return i;
else return -1;
}
int main()
{
Stu sa[] =
{
{12,"张三",170,200},
{22,"李三",170,200},
{32,"王三",170,200},
{42,"刘三",170,200},
{52,"许三",170,200},
{62,"黄三",170,200}
};
int a = binSearch(sa,6,42);
printf("%d \n",a);
if(a >= 0)
{
printf("%s\n",sa[a].name);
}
a = binSearch(sa,6,142);
printf("%d \n",a);
if(a >= 0)
{
printf("%s\n",sa[a].name);
}
a = seqSearch(sa,6,52);
if(a >= 0)
{
printf("%s\n",sa[a].name);
}
return 0;
}
输出:
3
刘三
-1
许三
5. Java实现
package tv.zhangjia.search;
class Student {
public int id;
public String name;
public int height;
public int weight;
public Student(int id, String name, int height, int weight) {
super();
this.id = id;
this.name = name;
this.height = height;
this.weight = weight;
}
}
public class BinSearch {
public static int binSearch(Student[] sa, int key) {
int low = 0, high = sa.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
int k = sa[mid].id;
if (key == k) {
return mid;
} else if (key > k) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return -1;
}
public static void main(String[] args) {
Student[] sa = new Student[5];
sa[0] = new Student(11, "张三", 170, 110);
sa[1] = new Student(21, "李三", 170, 110);
sa[2] = new Student(33, "王三", 170, 110);
sa[3] = new Student(42, "刘三", 170, 110);
sa[4] = new Student(51, "胡三", 170, 110);
int a = binSearch(sa, 42);
System.out.println(a);
if (a >= 0) System.out.println(sa[a].name);
a = binSearch(sa, 52);
System.out.println(a);
if (a >= 0) System.out.println(sa[a].name);
}
}
四. 二叉搜索树
1. 基本概念
二叉树搜索树是一棵空树或者是具有以下性质的二叉树:
- 每个结点都有一个作为搜索依据的关键码(key),所有的结点的关键码互不相同
- 如果存在左子树,则左子树上所有的结点的关键码都小于根结点的关键码
- 如果存在右子树,则右子树上所有的结点的关键码都大于根结点的关键码
- 树中任何结点的左子树中所有结点的值均比该结点小,右子树中所有结点的值均比该结点大
- 对二叉搜索树进行中序遍历即得到一个递增排序的序列
- 左子树和右子树也是二叉搜索树,举例如下:
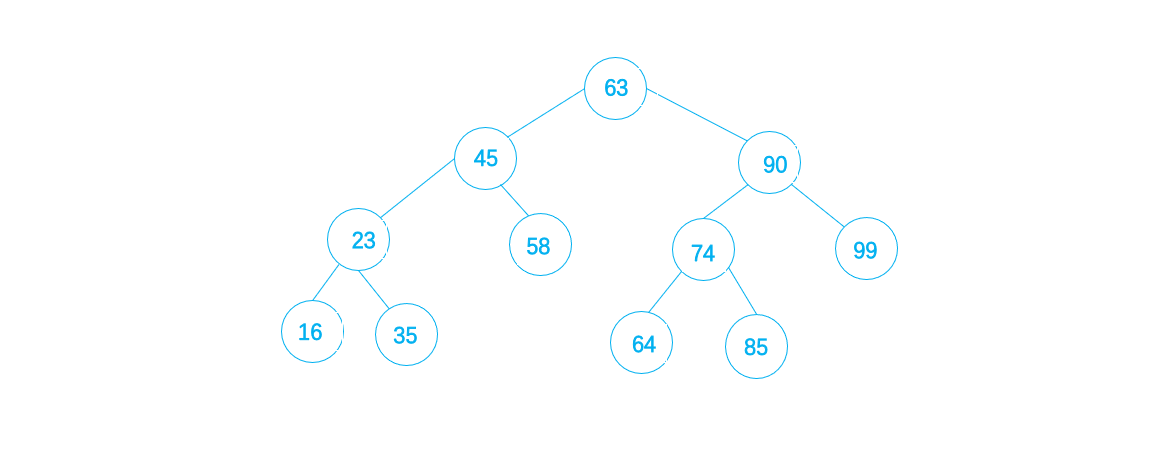
可以看出,63的左子树中,最大的58也比63小,而63的右子树中,最小的64也比63大
同时,关键码事实上是结点所保存元素中的某个域的值,它能唯一的表示这个结点,因此,如果对一个一棵二叉搜索树进行中序遍历就可以从小到大的顺序将关键码排列起来,所说也称二叉搜索树为二叉排序树
以上图为例,中序遍历的结果为:16 23 35 45 58 63 64 74 85 90 99 ,正好是所有关键码的从小到大排列
2. 二叉搜索树的插入和建立
在一棵二叉排序树中插入值为k的结点,步骤如下:
- 若二叉排序树为空,则生成值为k的新结点s,同时将新结点s作为根结点插入。
- 若k小于根结点的值,则在根的左子树中插入值为k的结点。
- 若k大于根结点的值,则在根的右子树中插入值为k的结点。
- 若k等于根结点的值,表明二叉排序树中已有此关键字,则无须插入。
举例(考试重点):
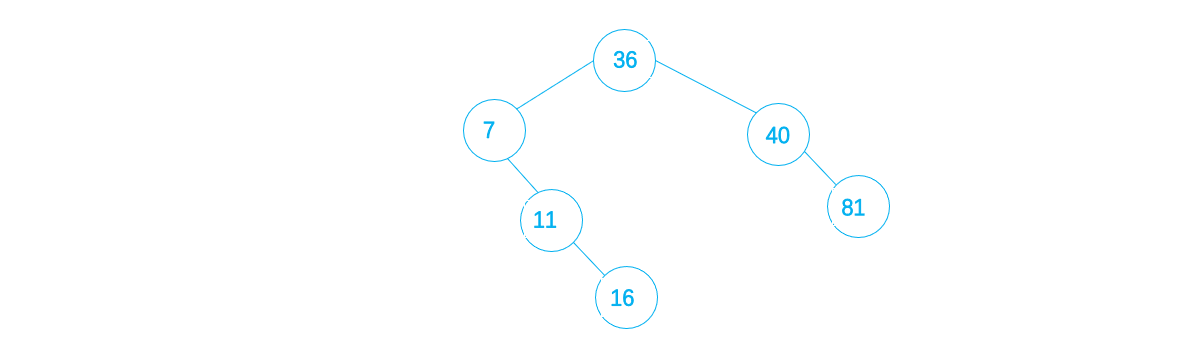
36,7,40,11,16,81,22,8,14
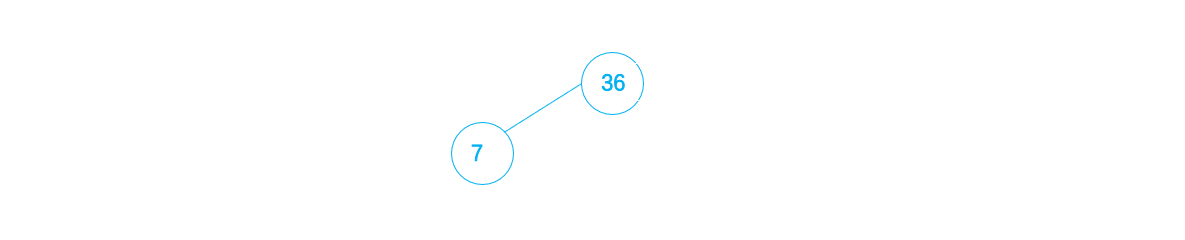
1. 首先,二叉排序树为空,则将36作为根结点插入
2. 接下来,7 < 36 ,则将7作为36的左子插入
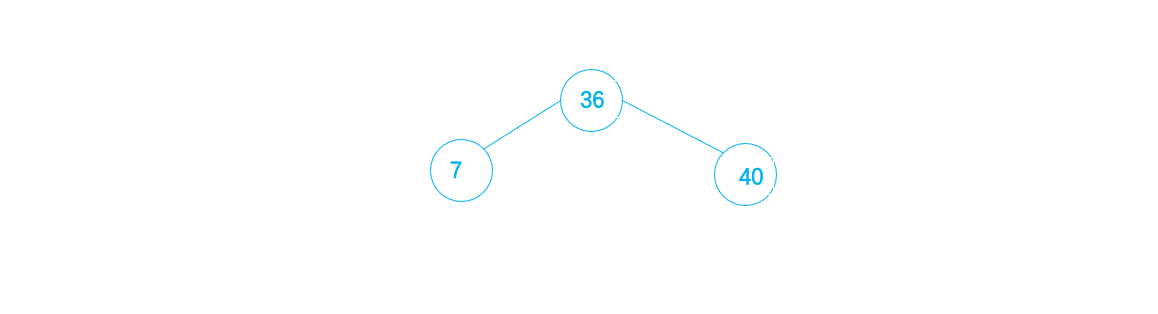
3. 而40 > 36 ,则将40作为36的右子插入
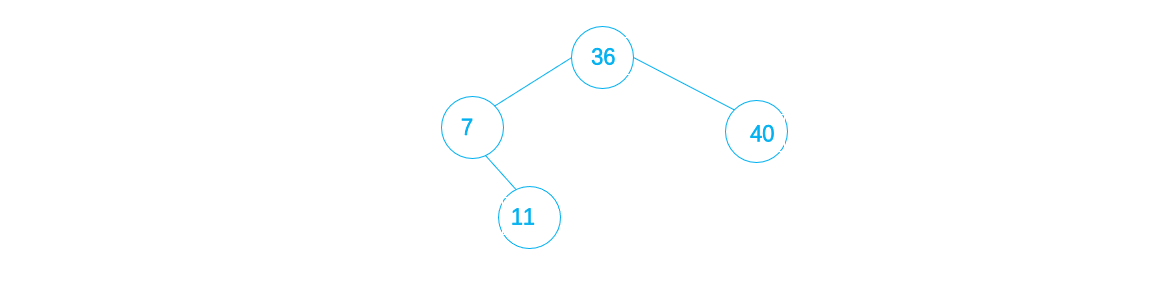
4. 11 < 36 且11 > 7 ,则将11作为7的右子插入
5. 16 <36, 且16 > 11 > 7 ,则将16作为11的右子插入
6. 81 > 36,且81 > 40 ,则将81作为40的右子插入
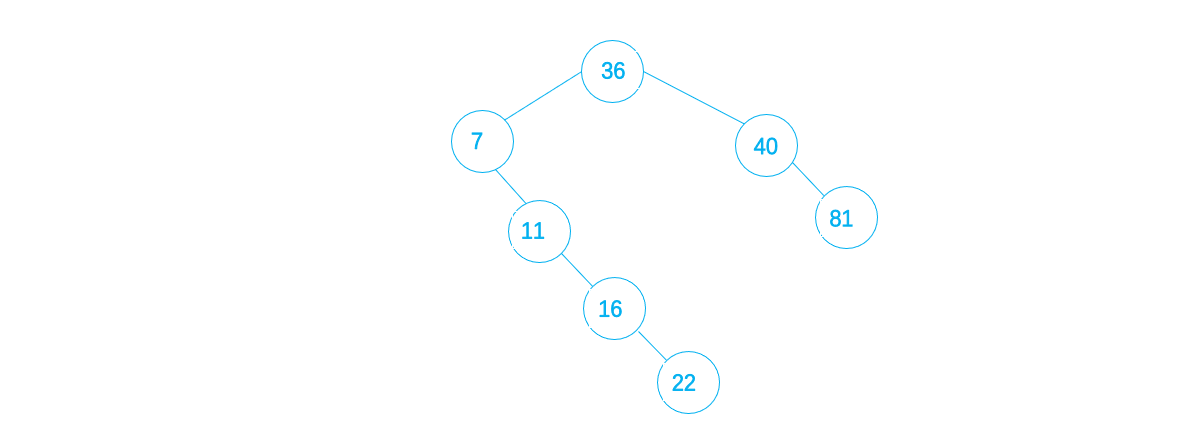
7. 22 < 36,且22 >7 ,且22 > 11 ,且22 > 16 ,则将22作为16的右子插入
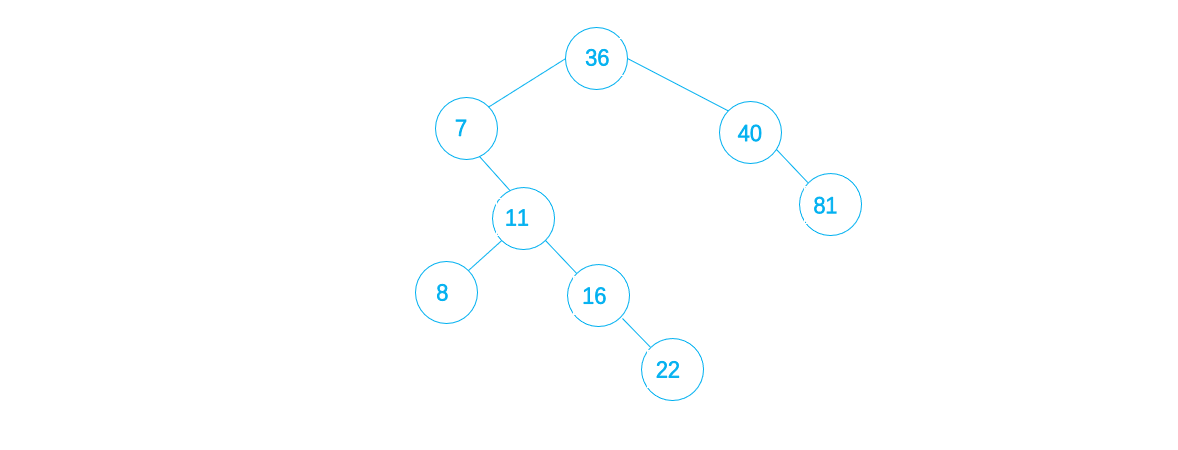
8. 8 < 36,且 8 > 7,且 8 < 11 ,则将8 作为11 的左子插入
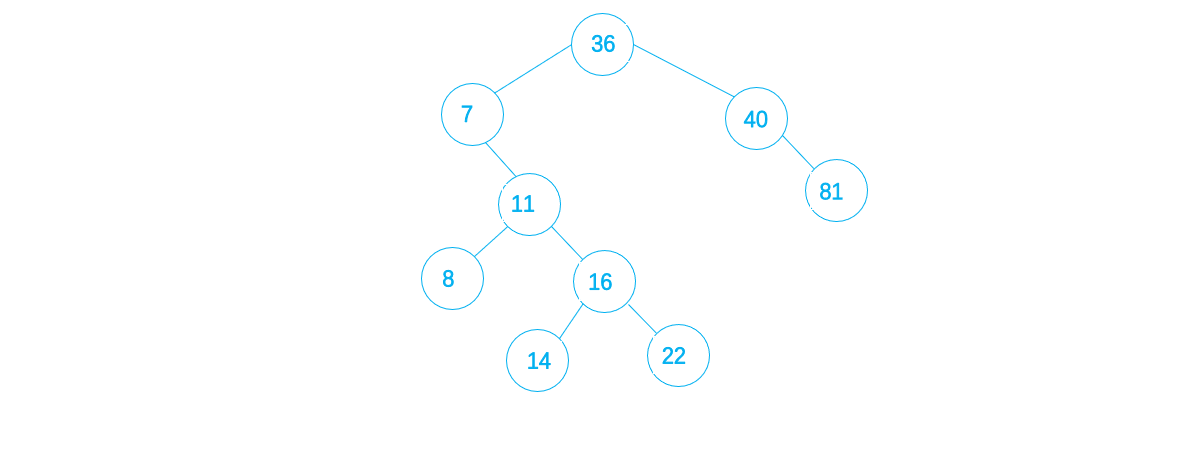
9. 14 < 36,且14 > 7,且14 > 11 ,且 14 < 16 ,则将14 作为16 的左子插入,完成
3.二叉排序树的查找过程
查找给定值k的过程如下:
- 若二叉排序树为空,则表明查找失败,返回空指针;否则,若给定值k等于根结点的值,则表明查找成功,返回根结点;
- 若给定值k小于根结点的值,则继续在根的左子树中查找;
- 若给定值k大于根结点的值,则继续在根的右子树中查找。
这是一个递归查找过程。
4. 二叉排序树的删除
二叉搜索树删除一个结点的时候,必须将因删除结点而断开的二叉链表重新链接起来,同时保证二叉搜索树的性质不会失去,性能不会降低,还需要防止重新链接后树的高度不能增加,二叉排序树的删除分为三种情况:
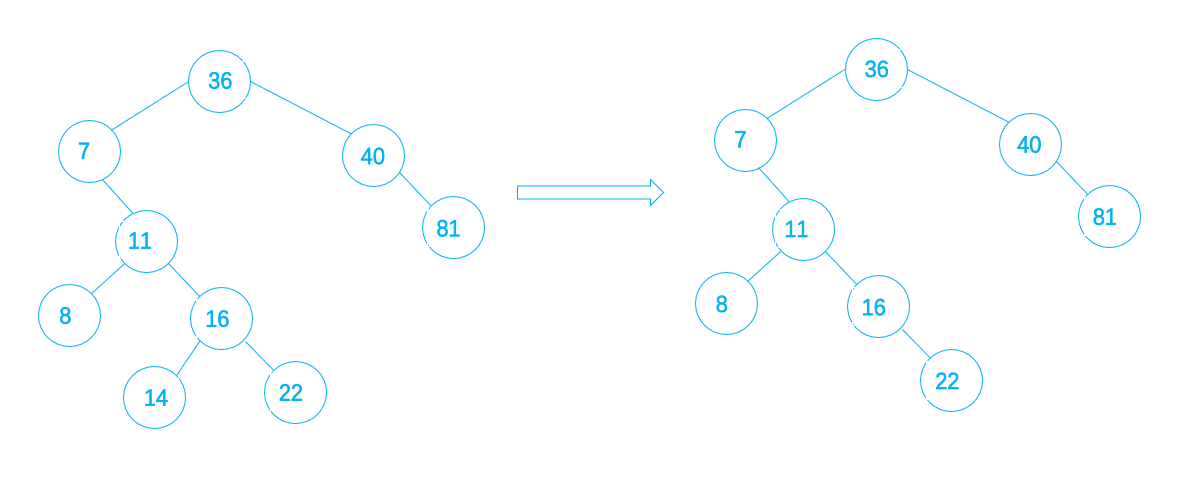
4.1 删除叶节点
叶节点的删除非常简单,只需要将其父结点指向它的指针清零,然后释放它就可以了,如下图,将14这个叶结点删除
4.2 删除单分支结点
什么是单分支结点呢,就是一个结点只有左子或者右子
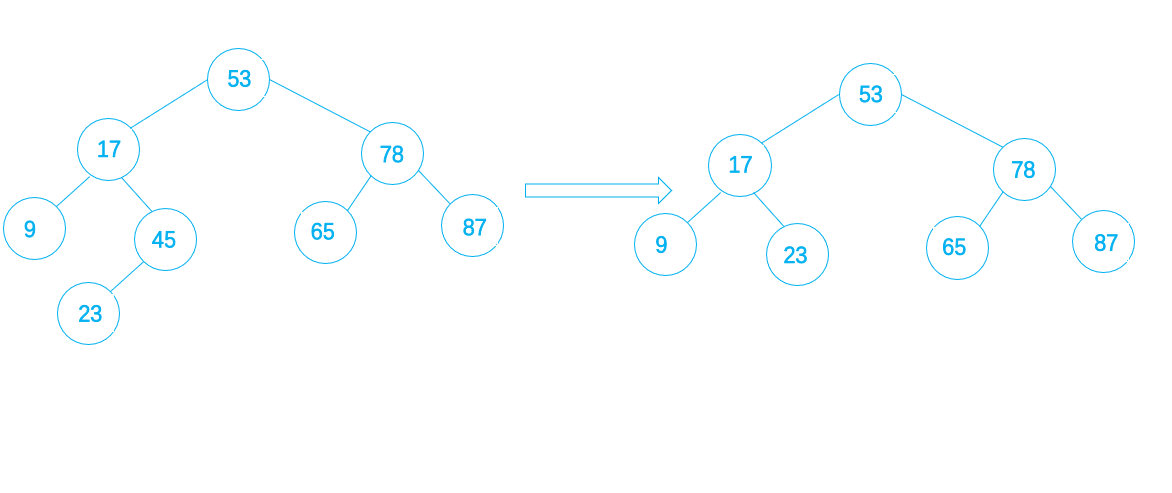
如果只有左子,则删除该单分支节点后,可以拿它的左子女结点顶替它的位置,再释放它,例如下图,将45这个单分支节点删除
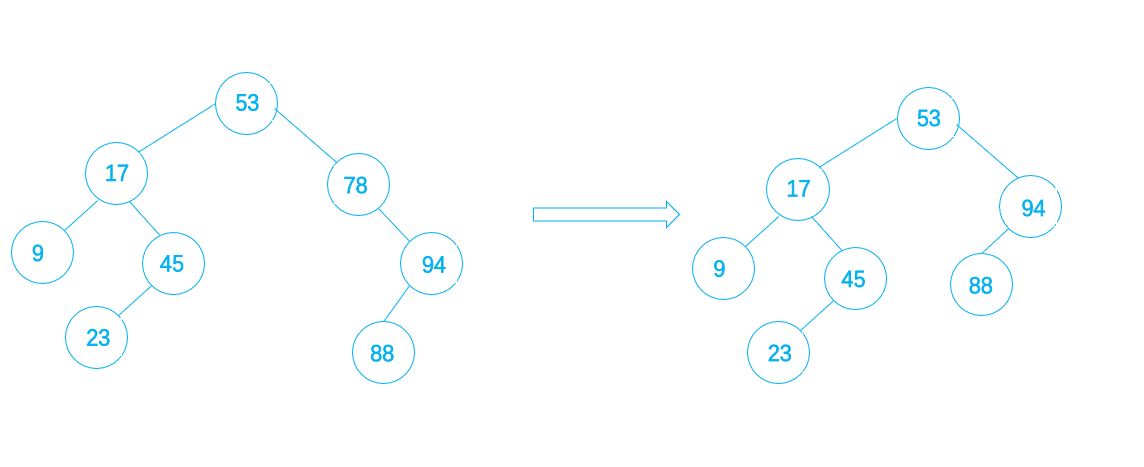
如果只有右子,则删除该单分支节点后,可以拿它的右子女结点顶替它的位置,再释放它,例如下图,将78这个单分支节点删除
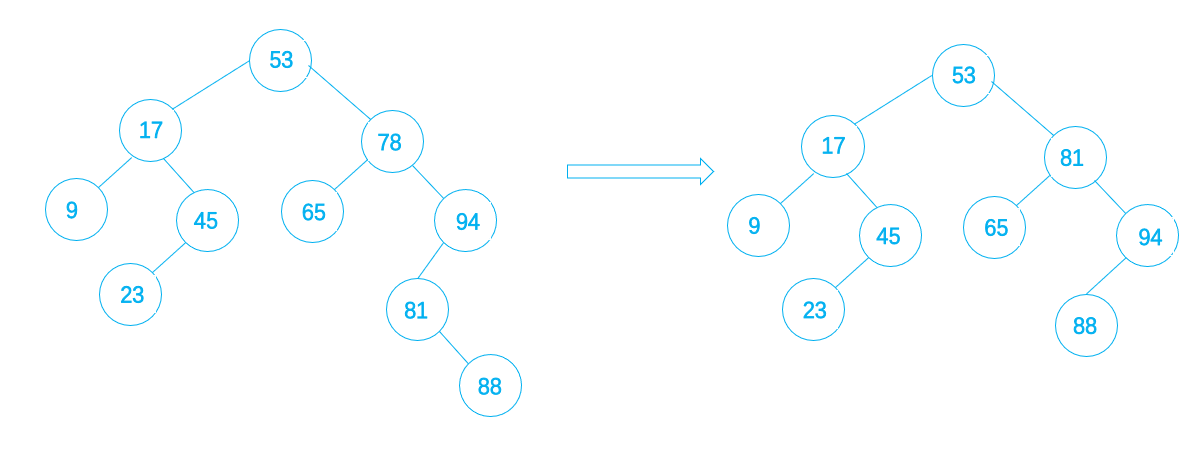
4.3 删除双分支结点
如果要删除的是双分支结点,那么被删除的结点的左子、右子树都不为空,可以在它的右子树中寻找中序下的第一个结点(关键码最小的那个),用它的值填补到被删除的结点中,再来处理这个结点的删除问题,这是一个递归的处理,例如下图中想要删除关键码为78的结点,它的左、右子都不为空,在它的右子树中找中序下的第一个结点,关键码为81,这个结点左子树为空,用它的右子树(关键码为88)代替它的位置就可以了






请登录之后再进行评论