习题:1.1.33
矩阵库,编写一个Matrix库,并实现以下API:
要点分析
一. 向量点乘
向量点乘又叫向量的内积、数量积,又分为代数定义和几何定义等,这里以代数定义为主[1]:
二. 矩阵乘法
- 当矩阵A的列数等于矩阵B的行数时,A与B可以相乘,等于C。
- 矩阵C的行数等于矩阵A的行数,C的列数等于B的列数。
- 乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和[2]
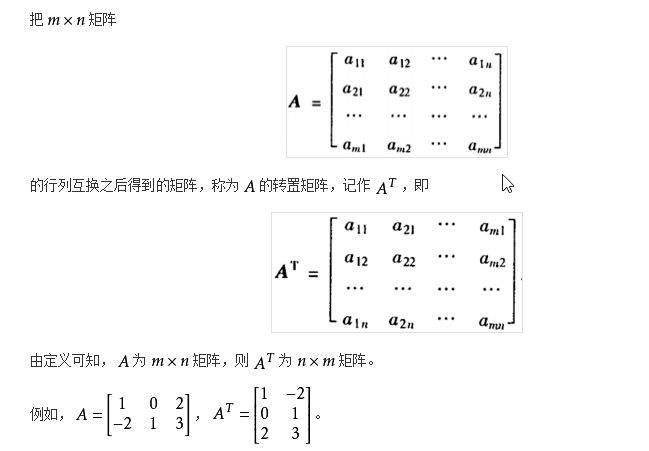
三. 转置矩阵
将矩阵的行列互换得到的新矩阵称为转置矩阵,转置矩阵的行列式不变 [3]:
四. 矩阵和向量之积
矩阵乘以向量的计算的方式如下[4]:
- 当矩阵A的列数等于向量的行数时,A与B可以相乘,等于C。
- 矩阵C的行数等于矩阵A的行数,C的列数等于向量的列数。
五. 向量和矩阵之积
- 当矩阵A的列数等于向量的行数时,A与B可以相乘,等于C。
- 矩阵C的行数等于矩阵A的行数,C的列数等于向量的列数。
六. 获取二维数组行列长度方法
public class Test {
public static void main(String[] args) {
int[][] a = new int[3][6];
System.out.println("行数为:" + a.length);
System.out.println("列数为:" + a[0].length);
}
}
输出:
行数为:3
列数为:6
参考答案
为了最后输出的时候方便,我把矩阵和向量以及向量和矩阵的积都用了二维数组来表示,因为这样可以在输出的时候输出一行或者一列。
public class Matrix {
public static double dot(double[] x, double[] y) {
if(x.length != y.length) {
System.out.println("Error!");
return 0;
}
double sum = 0;
for (int i = 0; i < x.length; i++) {
sum += x[i] * y[i];
}
return sum;
}
public static double[][] mult(double[][] a, double [][] b) {
if(a[0].length != b.length) {
System.out.println("Error!");
return null;
}
double[][] c = new double[a.length][b[0].length];
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < b[0].length; j++) {
for (int k = 0; k < b.length; k++) {
c[i][j] += a[i][k] * b[k][j];
}
}
}
return c;
}
public static double[][] transpose(double[][] a) {
double[][] c = new double[a[0].length][a.length];
for (int i = 0; i < a[0].length; i++) {
for (int j = 0; j < a.length; j++) {
c[i][j] = a[j][i];
}
}
return c;
}
public static double[][] mult(double[][] a, double[] x ) {
if(a[0].length != x.length) {
System.out.println("Error!!");
return null;
}
double[][] c = new double[a.length][1];
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a[0].length; j++) {
c[i][0] += a[i][j] * x[j];
}
}
return c;
}
public static double[][] mult(double[] y, double[][] a ) {
if(y.length != a.length) {
System.out.println("Error!!!");
return null;
}
double[][] c = new double[1][a[0].length];
for (int j = 0; j < a[0].length; j++) {
for (int k = 0; k < a.length; k++) {
c[0][j] += y[k] * a[k][j];
}
}
return c;
}
public static void print(double[][]a) {
if(a != null) {
for (int i = 0; i < a.length; i++) {
for (int j = 0; j < a[0].length; j++) {
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
}
public static void main(String[] args) {
double []a = {1,2};
double []b = {3,4};
System.out.println(dot(a,b));
System.out.println("_____________________________________");
double[][] A = {{1,2,3},{4,5,6}};
double[][] B = {{1,4},{2,5},{8,9}};
print(mult(A,B));
System.out.println("_____________________________________");
double[][] A2 = {{1,2},{3,4},{5,6},{7,8}};
print(transpose(A2));
System.out.println("_____________________________________");
double[][] A3 = {{1,2},{3,4},{5,6},{7,8}};
double[] B3 = {1,2};
print(mult(A3,B3));
System.out.println("_____________________________________");
double[] A4 = {1,2,3,4};
double[][] B4 = {{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
print(mult(A4,B4));
System.out.println("_____________________________________");
}
}
参考资料
[1] 百度百科:点积
[2] 百度百科:矩阵乘法
[3] 百度百科:转置矩阵
[4] 机器学习笔记

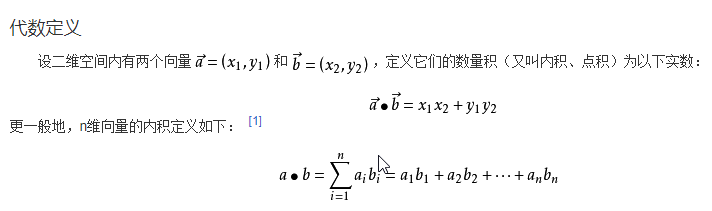

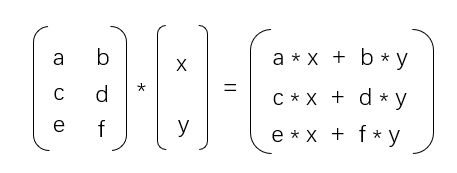
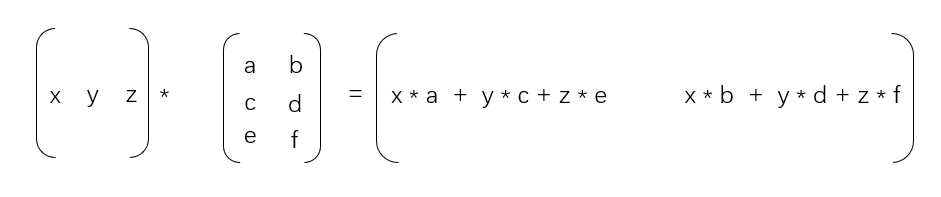


请登录之后再进行评论