习题1.2.3
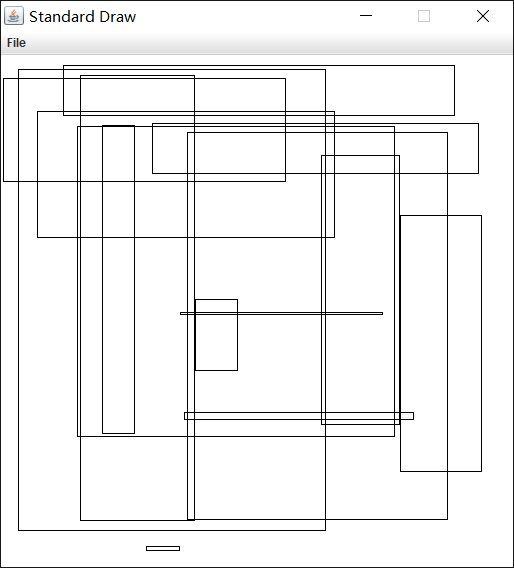
编写一个Interval2D的用例,从命令行接受参数N,min 和 max。生成 N 个随机的 2D 间隔,其宽度和高均匀地分布在单位正方形中的 min 和 max 之间。用StdDraw画出它们并打印出相交的间隔对的数量以及有包含关系的间隔对数量。
要点分析
1. Interval2d
关于Interval2d的API请查看课本第47页。简单来说,2D就是由两个1d的一维间隔创建而成。
其实本题的解释还是有些晦涩难懂的,用通俗的语言来讲,我们将题中的二维间隔看成一个长方形,就好懂多了。那么题目的意思也就是用Interval1d类生成两个长度为min~max之间的线段,然后用这两个线段分别作为长和宽组成一个长方形。然后重复上面的操作N次并将其画出。最后统计N个长方形有几个长方形是相交的,有几个是包含的就完成了。
2. 包含关系
在Interval2D中,提供了两个长方形是否相交的方法,也就是intersect(Interval2d that),所以这个问题实现起来是非常简单的
而本题的难度就在于,我们应该如何计算有包含关系的间隔对数量呢?
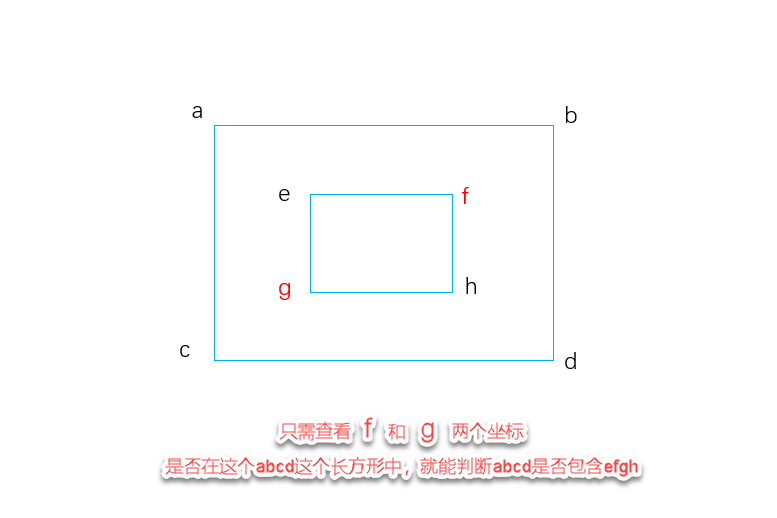
Interval2D给出的contains(Point2D p)方法,是用于计算一个点p是否包含在该长方形内,而且我们要计算的一个长方形是否包含在另一个长方形内,该方法似乎用不上,其实不然,我们只需要确认一个长方形的两个点的位置,就可以判断这个长方形的位置,如下图:
参考答案
import edu.princeton.cs.algs4.*;
/**
* @description: Interval2d用例
* @author: ZhangJia
* @create: 2018-08-02 17:01
**/
public class Three {
public static void Ini_Interval(int N, double min, double max, Interval2D[] i,Point2D[] p1,Point2D[] p2) {
StdDraw.setXscale(min, max);
StdDraw.setYscale(min, max);
for (int j = 0; j < N; j++) {
double a = StdRandom.uniform(min,max);
double b = StdRandom.uniform(min,max);
double c, d,e,f;
c = (a > b ? b : a);
d = (a > b ? a : b);// c <= d ,否则会报错
Interval1D x = new Interval1D(c,d); //创建一个一维间隔
a = StdRandom.uniform(min,max);
b = StdRandom.uniform(min,max);
e = (a > b ? b : a);
f = (a > b ? a : b);
Interval1D y = new Interval1D(e,f); //创建一个一维间隔
p1[j] = new Point2D(c, d);
p2[j] = new Point2D(c, d);
i[j] = new Interval2D(x,y);// 利用上面创建的两个一维间隔创建一个二维间隔
i[j].draw(); //用STDDraw画出该二维间隔
}
}
public static void print(Interval2D[] i) {
int count = 0;
for (int j = 0; j < i.length - 1; j++) {
for (int k = j + 1; k < i.length; k++) {
if(i[j].intersects(i[k])) {
count++;
}
}
}
System.out.println("相交的间隔对数量为:" + count);
}
public static void print_contain(Interval2D[] i,Point2D[] p1,Point2D[] p2) {
int count = 0;
for (int j = 0; j < i.length ; j++) {
for (int k = j ; k < i.length; k++) {
if (j != k && i[j].contains(p1[k]) && i[j].contains(p2[k])) {
count++;
}
}
}
System.out.println("相交的间隔对数量为:" + count);
}
public static void main(String[] args) {
int N = Integer.parseInt(args[0]);
double min = Double.parseDouble(args[1]);
double max = Double.parseDouble(args[2]);
Interval2D[] i = new Interval2D[N];
Point2D[] p1 = new Point2D[N];
Point2D[] p2 = new Point2D[N];
Ini_Interval(N,min,max,i,p1,p2);
print(i);
print_contain(i,p1,p2);
}
}
输入N = 15,min = 0,max = 0.8,输出:
相交的间隔对数量为:51
包含关系的间隔对数量为:8
另外我发现,如果a 包含 b则intersect(Interval2d that)方法也会将a和b看成相交,比如:
import edu.princeton.cs.algs4.Interval1D;
import edu.princeton.cs.algs4.Interval2D;
import edu.princeton.cs.algs4.Point2D;
public class Test2 {
public static void main(String[] args) {
int N = 2;
Interval2D[] i = new Interval2D[N];
Point2D[] p1 = new Point2D[N];
Point2D[] p2 = new Point2D[N];
Interval1D i1 = new Interval1D(0.2, 0.3);
Interval1D i2 = new Interval1D(0.3, 0.5);
i[0] = new Interval2D(i1, i2);
p1[0] = new Point2D(0.2, 0.3);
p2[0] = new Point2D(0.3, 0.5);
i[0].draw();
/*
Interval1D i3 = new Interval1D(0.1,0.25);
Interval1D i4 = new Interval1D(0.36,0.4);
i[1] = new Interval2D(i3,i4);
p1[1] = new Point2D(0.1, 0.36);
p2[1] = new Point2D(0.25, 0.4);
i[1].draw();
*/
Interval1D i5 = new Interval1D(0.05, 0.5);
Interval1D i6 = new Interval1D(0.1, 0.6);
i[1] = new Interval2D(i5, i6);
p1[1] = new Point2D(0.05, 0.5);
p2[1] = new Point2D(0.1, 0.6);
i[1].draw();
print(i);
print_contain(i, p1, p2);
}
public static void print(Interval2D[] i) {
int count = 0;
//注意:比如a和b相交,则相交的总数加1,而且不用再判断b和a是否相交了。
for (int j = 0; j < i.length - 1; j++) {
for (int k = j + 1; k < i.length; k++) {
if (i[j].intersects(i[k])) {
count++;
}
}
}
System.out.println("相交的间隔对数量为:" + count);
}
public static void print_contain(Interval2D[] i, Point2D[] p1, Point2D[] p2) {
int count = 0;
//注意:比如a包含b,则包含的总数加1,但是如果a不包含b,必须还得判断b是否包含a
for (int j = 0; j < i.length; j++) {
for (int k = 0; k < i.length; k++) {
// 判断
if (j != k && i[j].contains(p1[k]) && i[j].contains(p2[k])) {
count++;
}
}
}
System.out.println("包含关系的间隔对数量为:" + count);
}
}
输出:
相交的间隔对数量为:1
包含关系的间隔对数量为:1
值得注意的是:
比如长方形a和长方形b不相交,就不用再判断b和a是否相交了。
但是如果长方形a不包含b,则必须还得判断b是否包含a
在参考jimmysuncpt前辈的答案时,他可能不小心打错了,没有再判断b是否包含a,导致有时候的结果会不正确。
下面给出他的答案:
package com.jimmysun.algorithms.chapter1_2;
import edu.princeton.cs.algs4.Interval1D;
import edu.princeton.cs.algs4.Interval2D;
import edu.princeton.cs.algs4.Point2D;
import edu.princeton.cs.algs4.StdDraw;
import edu.princeton.cs.algs4.StdRandom;
public class Ex03 {
public static void main(String[] args) {
int N = Integer.parseInt(args[0]);
double min = Double.parseDouble(args[1]);
double max = Double.parseDouble(args[2]);
StdDraw.setXscale(min, max);
StdDraw.setYscale(min, max);
Point2D[] leftTopPoints = new Point2D[N];
Point2D[] rightBottomPoints = new Point2D[N];
Interval2D[] intervals = new Interval2D[N];
for (int i = 0; i < N; i++) {
double a = StdRandom.uniform(min, max);
double b = StdRandom.uniform(min, max);
double left, right, top, bottom;
Interval1D x, y;
if (a < b) {
left = a;
right = b;
} else {
left = b;
right = a;
}
x = new Interval1D(left, right);
a = StdRandom.uniform(min, max);
b = StdRandom.uniform(min, max);
if (a < b) {
top = a;
bottom = b;
} else {
top = b;
bottom = a;
}
y = new Interval1D(top, bottom);
leftTopPoints[i] = new Point2D(left, top);
rightBottomPoints[i] = new Point2D(right, bottom);
intervals[i] = new Interval2D(x, y);
intervals[i].draw();
}
int containNum = 0, intervalNum = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N; j++) {
if (j > i && intervals[i].intersects(intervals[j])) {
intervalNum++;
}
if (j != i && intervals[i].contains(leftTopPoints[j]) && intervals[i].contains(rightBottomPoints[j])) {
containNum++;
}
}
}
System.out.println("Interval count: " + intervalNum);
System.out.println("Contain count: " + containNum);
}
}
我写了一个测试用例:
import edu.princeton.cs.algs4.Interval1D;
import edu.princeton.cs.algs4.Interval2D;
import edu.princeton.cs.algs4.Point2D;
public class Test3 {
public static void main(String[] args) {
int N = 2;
Interval2D[] intervals = new Interval2D[N];
Point2D[] leftTopPoints = new Point2D[N];
Point2D[] rightBottomPoints = new Point2D[N];
Interval1D i1 = new Interval1D(0.2, 0.3);
Interval1D i2 = new Interval1D(0.3, 0.5);
intervals[0] = new Interval2D(i1, i2);
leftTopPoints[0] = new Point2D(0.2, 0.3);
rightBottomPoints[0] = new Point2D(0.3, 0.5);
intervals[0].draw();
/*
Interval1D i3 = new Interval1D(0.1,0.25);
Interval1D i4 = new Interval1D(0.36,0.4);
intervals[1] = new Interval2D(i3,i4);
leftTopPoints[1] = new Point2D(0.1, 0.36);
rightBottomPoints[1] = new Point2D(0.25, 0.4);
intervals[1].draw();
*/
Interval1D i5 = new Interval1D(0.05, 0.5);
Interval1D i6 = new Interval1D(0.1, 0.6);
intervals[1] = new Interval2D(i5, i6);
leftTopPoints[1] = new Point2D(0.05, 0.5);
rightBottomPoints[1] = new Point2D(0.1, 0.6);
intervals[1].draw();
int containNum = 0, intervalNum = 0;
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N; j++) {
if (j > i && intervals[i].intersects(intervals[j])) {
intervalNum++;
}
if (j != i && intervals[i].contains(leftTopPoints[j]) && intervals[i].contains(rightBottomPoints[j])) {
containNum++;
}
}
}
System.out.println("Interval count: " + intervalNum);
System.out.println("Contain count: " + containNum);
}
}
输出:
Interval count: 1
Contain count: 0
可以看到,包含的数量是有问题的,所以不能采用这种遍历的方法。
参考资料
本题的包含关系代码参考了jimmysuncpt前辈的答案


请登录之后再进行评论