一. 前言
Kruskal算法又称克鲁斯卡尔算法,在离散数学中又叫避圈法,是一种用来查找最小生成树的算法,由Joseph Kruskal在1956年发表,用来解决同样问题的还有Prim算法,我们先来引入最小生成树的概念
二. 最小生成树
设无向连通带权图G = <V,E,W>,T是G的一棵生成树,T的各边权之和称为T的权,记作W(T),G的所有生成树中权最小的生成树,称为G的最小生成树,最小生成树若有n个结点,则有n-1条边
三. Kruskal算法
1. 设n阶无向连通带权图G = <V,E,W>有m条边,将m条边的权按照从小到大的顺序排列,设为e1,e2,……em
2. 取e1 在T中,然后依次检查e2,e3……em,如果ej(j>=2)与已在T中的边不能构成回路,则取ej在T中,否则去掉ej
3. 当算法停止时,得到的T就是G的最小生成树
另外值得注意的是:
使用不同的遍历图的方法,可以得到不同的生成树;
从不同的顶点出发,也可能得到不同的生成树。
四. 举例
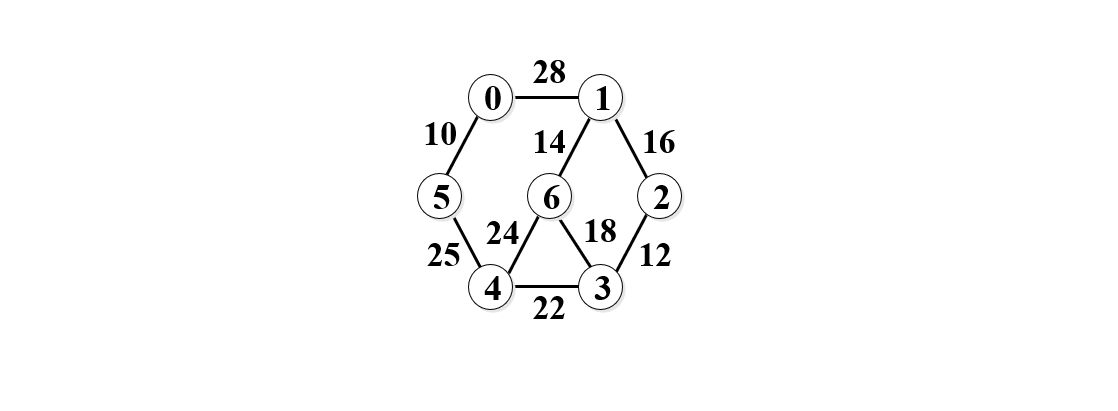
1. 用KruKal算法,求下图的最小生成树
2. 首先将权值从小到大排列:10 < 12 < 14 < 16 < 18 < 22 < 24 < 25 < 28
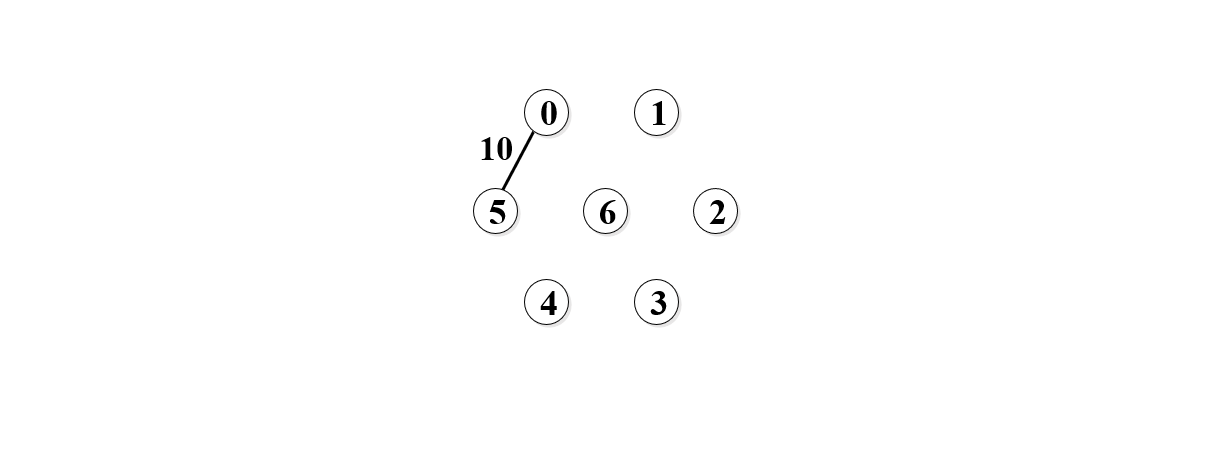
3. 接下来,先取权值最小的10,如下图
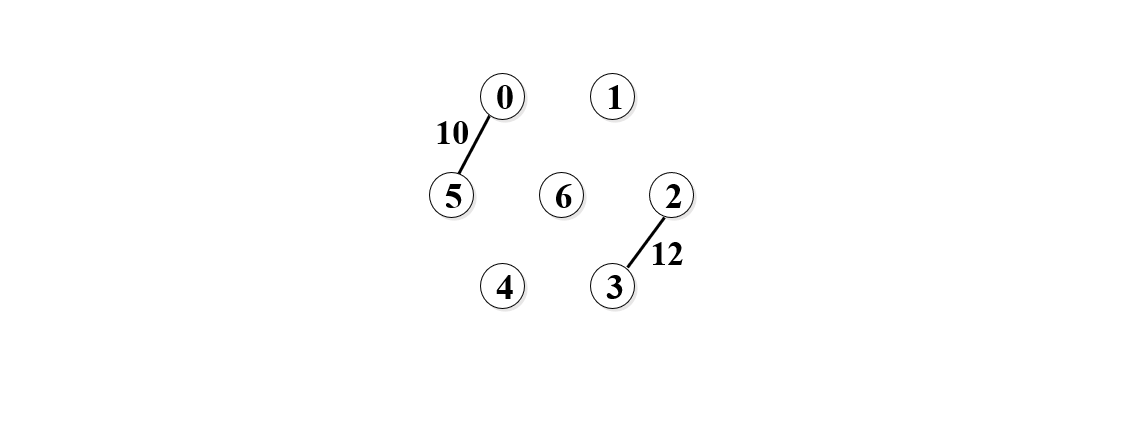
4. 再取12,如下图
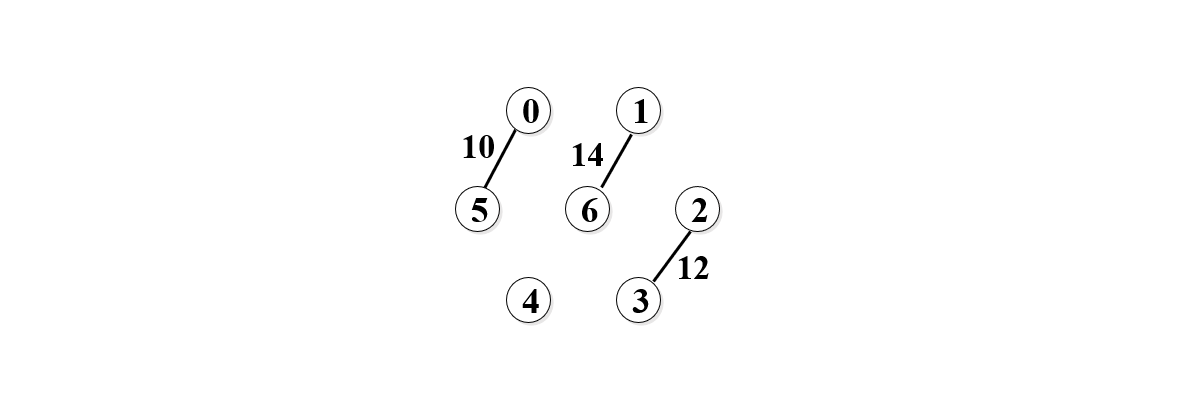
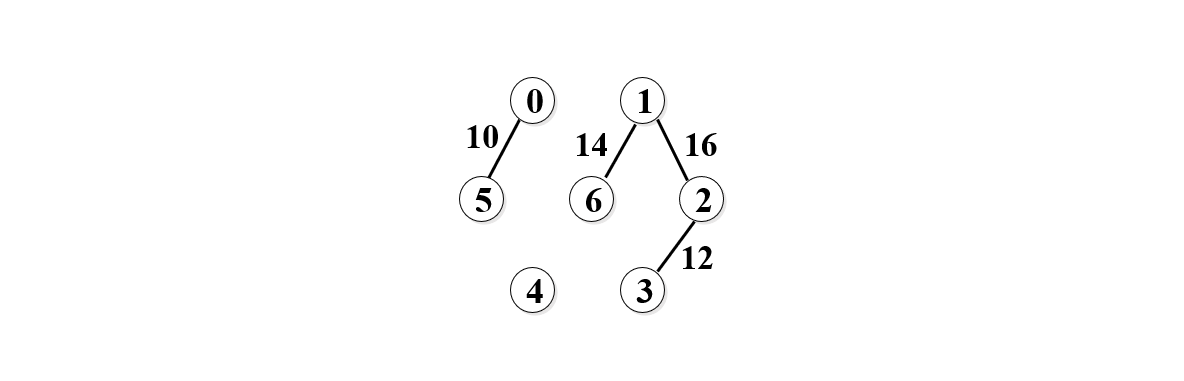
5. 再取14,如下图
6. 再取16,如下图
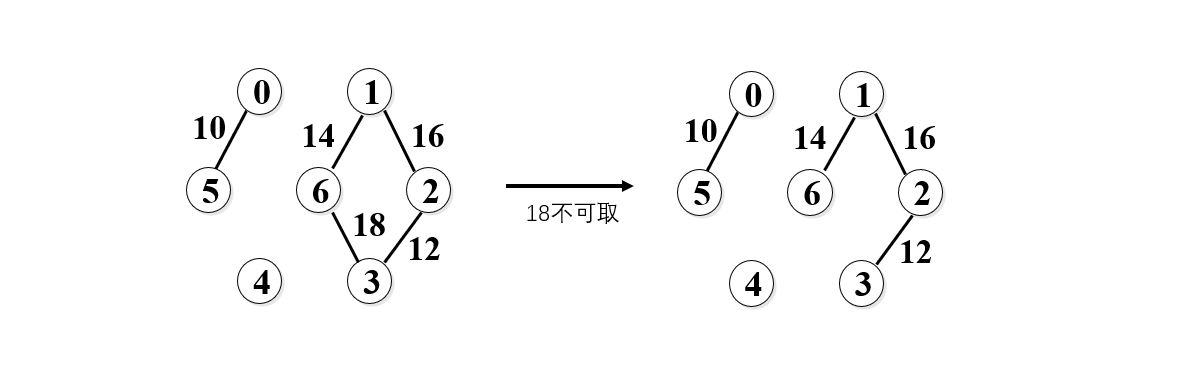
7. 再取18,但是我们发现加上18后,构成了一个回路,所以18不可取,如下图
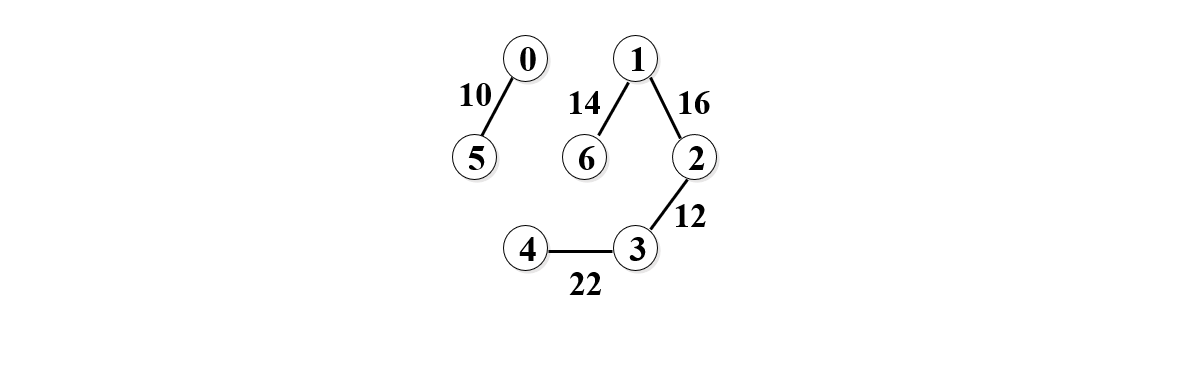
8. 再取22,如下图
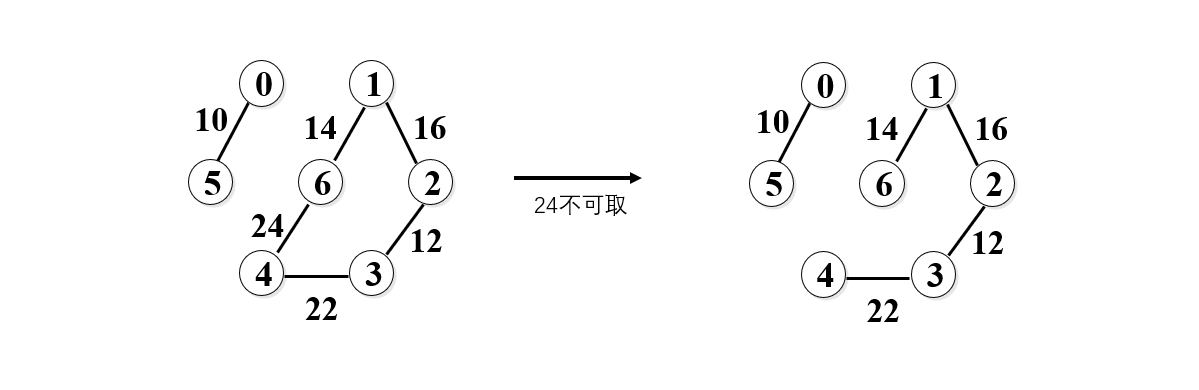
9. 再取24,但是我们发现加上24后,构成了一个回路,所以24不可取,如下图
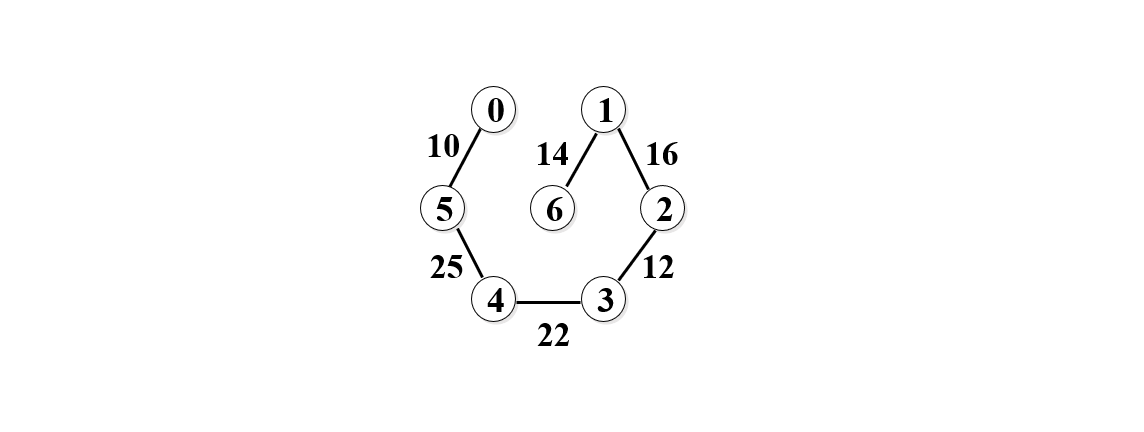
10. 再取25,如下图
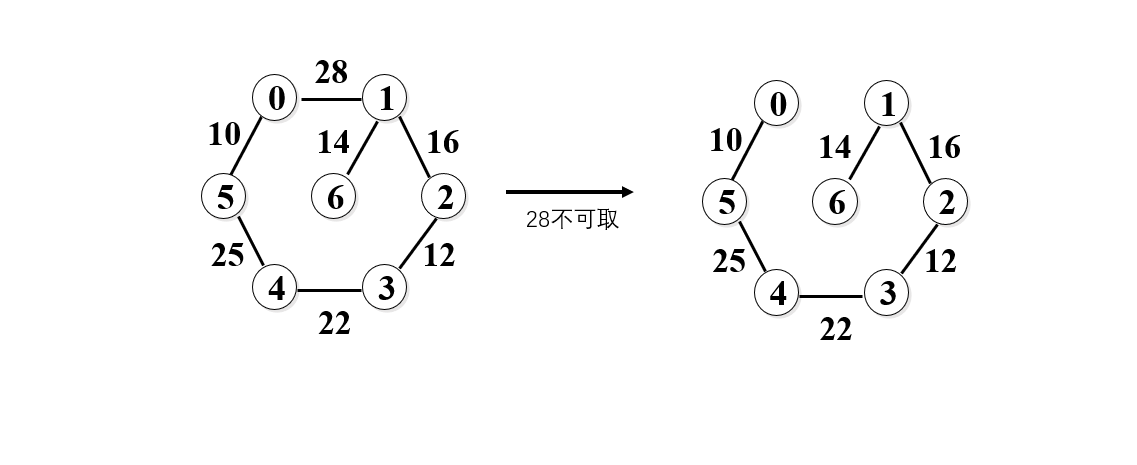
11. 再取28,但是我们发现加上28后,构成了一个回路,所以28不可取,至此,最小生成树完成,如下图


请登录之后再进行评论