一. 前言
在前面我们讲解了Kruskal算法求最小生成树的过程,这里我们再来讲解下用Prim算法如何求最小生成树
二. Prim算法
Prim算法是从单一顶点开始,普里姆算法按照以下步骤逐步扩大树中所含顶点的数目,直到遍及连通图的所有顶点,步骤如下:
1. 输入:一个加权连通图,其中顶点集合为V,边集合为E;
2. 初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {};
3. 重复下列操作,直到Vnew = V:
3.1 在集合E中选取权值最小的边(u, v),其中u为集合Vnew中的元素,而v则是V中没有加入Vnew的顶点(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
3.2 将v加入集合Vnew中,将(u, v)加入集合Enew中;
4. 输出:使用集合Vnew和Enew来描述所得到的最小生成树。
三. 举例
找了很多例子都表达的含糊不清,依旧找到维基百科的例子非常好,整理如下:
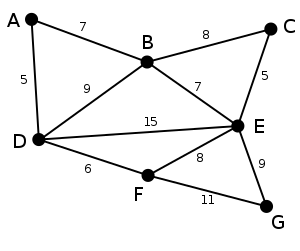
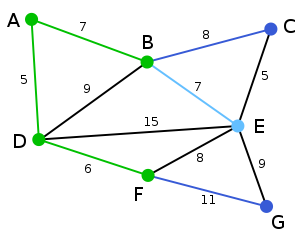
1. 以下面的图为例,每条边一侧的数字代表其权值。
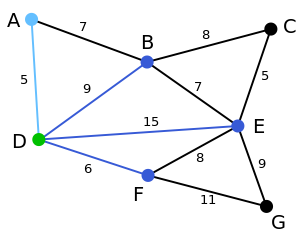
2. 顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点,因此将A及对应边AD以高亮表示
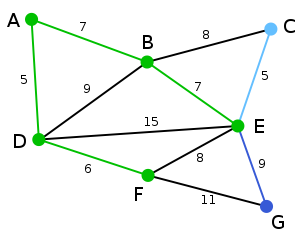
3. 下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F与相应边DF以高亮表示
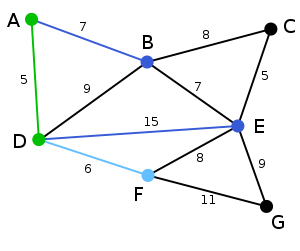
4. 算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。
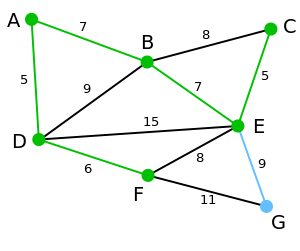
5. 在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。E最近,因此将顶点E与相应边BE高亮表示。
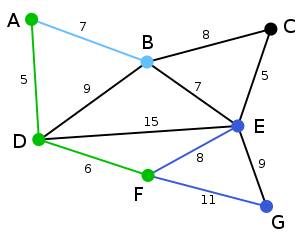
6. 这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C,并与边EC一同高亮表示。
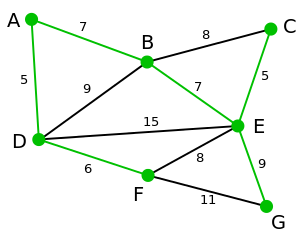
7. 顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故高亮表示G及相应边EG。
8. 现在,所有顶点均已被选取,图中绿色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。


请登录之后再进行评论